Bihar Board Class 9th Maths Solutions Chapter 11 Constructions Ex 11.1

Bihar Board Class 9th Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Questions and Answers.

BSEB Bihar Board Class 9th Maths Solutions Chapter 11 Constructions Ex 11.1

Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of Construction :

1. Draw a ray OA.
2. With its initial point O as centre and any radius, draw an arc CDE, cutting OA at C.
   
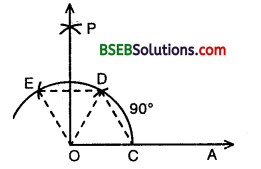
3. With centre C and same radius (as in step 2), draw an arc, cutting the arc CDE at D.
4. With D as centre and the same radius, draw an arc cutting the arc CDE at E.
5. With D and E as centres, and any. convenient radius (more than \(\frac { 1 }{ 2 }\) DE ), draw two arcs intersecting at P.
6. Join OP. Then ∠AOP = 90°.

Justification :
By construction, OC = CD = OD
∴ ∆ OCD is an equilateral triangle. So, ∠COD = 60°.
Again, OD = DE = EO
∴ ∆ ODE is also an equilateral triangle. So, ∠DOE = 60°.
Since OP bisects ∠DOE, so ∠POD = 30°.
Now, ∠AOP = ∠COD + ∠DOP = 60° + 30° = 90°.

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of Construction

1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc cutting OA at B.
   
3. With B as centre and same radius cut the previous drawn arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to ut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE. Then ∠AOF = 45°.

Justification :
By construction, ∠AOE = 90° and OF is the bisector of ∠AOE
∴ ∠AOF = \(\frac { 1 }{ 2 }\)∠AOE = \(\frac { 1 }{ 2 }\) x 90° = 45°.

Question 3.
Construct the angles of the following measurements :
(i) 30°
(ii) 22\(\frac { 1° }{ 2 }\)
(iii) 15°.
Solution:
(i) Steps of Construction :

• Draw a ray OA.
• With its initial point O as centre and anyx radius, draw an arc, cutting OA at C.
  
• With centre C and same radius (as in step 2). Draw an arc, cutting the arc of step 2 in D.
• With C and D as centres, and any convenient radius (more than \(\frac { 1 }{ 2 }\) CD), draw two arcs intersecting at B.
• Join OB. Then ∠AOB = 30°.

(ii) Steps of Construction :

• Draw an angle AOB = 90°.
• Draw the bisector OC of ∠AOB, then ∠AOC = 45°.
  
• Bisect ∠AOC, such that ∠AOD = ∠COD = 22.5°.
  Thus, ∠AOD = 22.5°.

(iii) Steps of Construction :

• Construct an ∠AOB = 60°.
• Bisect ∠AOB so that ∠AOC = ∠BOC = 30°.
  
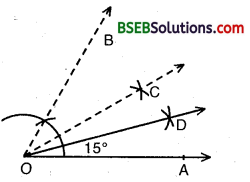
• Bisect ∠AOC, so that ∠AOD = ∠COD = 15°.
  Thus, ∠AOD = 15°.

Question 4.
Construct the following angles and verify by measuring them by a protractor :
(i) 75°
(ii) 105°
(iii) 135°
Solution:
(i) Steps of Construction :

• Draw a ray OA.
• Construct ∠AOB = 60°.
• Construct ∠AOP = 90°.
• Bisect ∠BOP so that
  
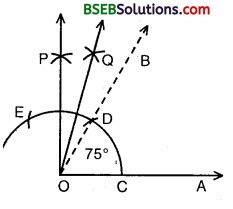
• So, we obtain ∠AOQ = ∠AOP + ∠BOQ = 60° + 15° = 75°.

Verification :
On measuring ∠AOQ, with the protractor, we find ∠AOQ – 75°.

(ii) Steps of Construction :

• Draw a line segment XY.
• Construct ∠XYT = 120° and ∠XYS = 90°, so that ∠SYT = ∠XYT – ∠XYS = 120° – 90° = 30°
  
• Bisect angle SYT, by drawing its bisector YZ.
• Then ∠XYZ is the required angle of 105°.

(iii) Steps of Construction :

• Draw ∠AOE = 90°. Then, ∠LOE = 90°.
  
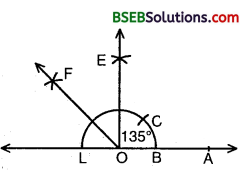
• Draw the bisector OF of ∠LOE.
• Then, ∠AOF = 135°.

 

Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
Let us draw an equilateral triangle of side 4.6 cm (say).
Steps of Construction :

1. Draw BC = 4.6 cm.
2. With B and C as centres and radii equal to BC = 4.6 cm, draw two arcs on the same side of BC, intersecting each- other at A.
   
3. Join AB and AC.
4. Then, ABC is the required equilateral triangle.

Justification :
Since by construction :
AB = BC = CA = 4.6 cm.
∴ ∆ ABC is an equilateral triangle.