Bihar Board Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.3 Text Book Questions and Answers.
BSEB Bihar Board Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.3
![]()
प्रश्न 1.
वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिन्दु भनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं को अधिकतम संख्या क्या है?
उत्तर:
वृत्तों के कई युग्म खींचने से सिद्ध होता है कि प्रत्येक गोड़े के दो उभयनिष्त बिन्दु ग्रेते हैं।
उभयनिष्ठ बिन्दुओं को अधिकतम संख्या भी दो है।
![]()
प्रश्न 2.
मान लीजिए आपको वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
उत्तर:
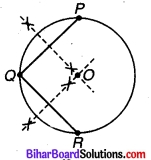
(1) वृत्त पर तीन बिन्दु P, Q तथा R है।
(2) PQ तथा QR को मिलाया।
(3) PQ तथा QR के लम्ब अर्द्धक खाँचे जो O पर प्रतियोद करते हैं। अत: O वृत्त का केन्द्र है।
![]()
प्रश्न 3.
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित है।
उत्तर:
दिया गया है: O तथा O’ केन्द्र वाले दो वृत्त एक दूसरे को बिन्दु A तथा B पर इस प्रकार प्रतिच्छेद करते हैं कि उभयनिष्ठ जीवा AB तथा दोनों के केन्द्रों के बीच का रेखाखण्ड OO’ है।
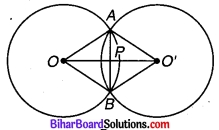
OO’ तथा AB परस्पर P पर प्रतिच्छेद करते हैं।
सिद्ध करना है : OO’, AB का लम्ब समद्विभानक है।
रचना : O’A, O’B, OA तथा OB को मिलाया।
उपपत्ति : ∆OAO’ स्था ∆OBO’ में,
OA = OB (विचार)
O’A = O’B (प्रिया)
तथा OO’ = OO’ (उभयनिष्ठ)
∆OAO’ ≈ ∆OBO’ (SSS नियम से)
⇒∠AOO’ = ∠BOO’
⇒ ∠AOP = ∠BOP ……. (1)
![]()
[∵ AOO’= ∠AOP तथा ∠BOP = BOO’]
∆AOP तथा ∆BOP में,
OA = OB (त्रिज्या)
तथा ∠AOP = ∠BOP (उभयनिष्ठ)
OP = OP समी. (1) से]
∆AOP ≈ ∆BOP (SAS नियम से)
⇒ AP = PB तथा ∠APO = ∠BPO
∠APO + ∠BPO = 180°
∴ 2∠APO = 180°
⇒ ∠APO = 90°
इसलिए AP = BP
तथा ∠APO = ∠BPO = 90°
अत: AB का लम्ब समद्विभाजक OO’ है।
![]()