Bihar Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.4 Textbook Questions and Answers.
BSEB Bihar Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.4
![]()
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Let O and O’ be the centres of the circles of radii 5 cm and 3 cm respectively and let PQ be them common chord.
We have OP = 5 cm, O’P = 3 cm and OO’ = 4 cm.
Since OP² = PO’² + O’O² [∵ 5² = 3² + 4²]
⇒ OOP is a right ∠d ∆, right angled as O’.

From (1) and (2), we have
2 x PL = 6 ⇒ PL = 3
We know that when two circles intersect at two points, then their centre lie on the perpendicular bisector of the common chord i.e., 00′ is the perpendicular bisector of AB.
∴ PQ = 2 x PL = (2 x 3) cm = 6 cm.
![]()
Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Given : AB and CD are chords of a circle with centre O. AB and CD intersect at P and AB = CD.
To prove : (i) AP = PD (ii) PB = CP.
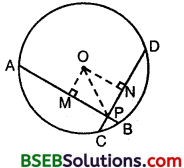
Construction : Draw OM ⊥ AB, ON ⊥ CD.
Join OP.
AM = MB = \(\frac { 1 }{ 2 }\)[Perpendicular from centre bisects the chord]
CN = ND = \(\frac { 1 }{ 2 }\) CD [Perpendicular from centre bisects the chord]
AM = ND and MB = CN s …(1) [∵ AB = CD (given)]
In As OMP and ONP, we have
OM = ON
[Equal chords of a circle are equidistant from the centre]
∠OMP = ∠ONP [∵ Each = 90°]
OP = OP [Common]
By RHS criterion of congruence,
∆ OMP = ∆ ONP
⇒ MP = PN … (2) [C.P.C.T.]
Adding (1) and (2), we have
AM + MP = ND + PN ⇒ AP = PD
Subtracting (2) from (1), we have
MP – MP = CN – PN
PB = CP
Hence, (i) AP = PD and (ii) PB = CP.
![]()
Question 3.
If two equal chords of a circle intersect within ‘ the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Given : AB and CD are chords of a circle with centre O. AB and CD intersect at P and AB = CD.
To prove : ∠OPE = ∠OPF.
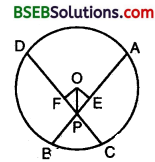
Construction : Draw OE ⊥ AB and OF ⊥ CD, Join OP.
Solution:
In ∆s OEP and OFP, we have
∠OEP = ∠OFP [∵ Each = 90°]
OP = OP
OE = OF [Equal chords of a circle are equidistant from the centre]
∴ By RHS criterion of congruence
∆ OEP ≅ ∆ OFP
⇒ ∠OPE = ∠OPF
![]()
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see figure).
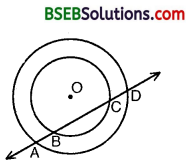
Solution:
Let OM be perpendicular from O on line l. We know that the perpendicular from the centre of a circle to a chord, bisects the chord.
Since BC is a chord of the smaller circle and OM ⊥ BC.
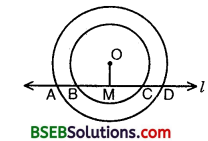
BM = CM … (1)
Again, AD is a chord of the larger circle and OM ⊥ AD.
∴ AM = DM … (2)
Subtracting (1) from (2), we get
AM – BM = DM – CM ⇒ AB = CD.
![]()
Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Let the three girls Reshma, Salma and Mandip are standing on the circle of radius 5 cm at points B, A and C respectively.

We know that if AB and AC are two equal chords of a circle, then the centre of the circle lies on the bisector of ∠BAC.
Here, AB = AC = 6 cm. So, the bisector of ∠BAC passes through the centre O i.e., OA is the bisector of ∠BAC.
Since the internal bisector of an angle divides the opposite sides in the ratio of the sides containing the angle. Therefore, M divides BC in the ratio 6 : 6 = 1 : 1 i.e., M is the middle point of BC.
Now, M is the mid-point of BC ⇒ OM ± BC.
In right ∠d A ABM, we have
AB² = AM² + BM²
⇒ 36 = AM² + BM²
⇒ BM² = 36 – AM² … (1)
In the right A OBM, we have
OB² = OM² + BM²
⇒ 25 = (OA – AM)² + BM²
⇒ BM² = 25 – (OA – AM)²
⇒ BM² = 25 – (5 – AM)² … (2)
From (1) and (2), we get
36 – AM² = 25 – (5 – AM)²
⇒ 11 – AM² + (5 – AM)² = 0
⇒ 11 – AM² + 25 – 10AM + AM² = 0
⇒ 10AM = 36
⇒ AM = 3.6
Putting AM = 36 in (1), we get
BM² = 36 – (3.6)² = 36 – 12.96
⇒ BM = \(\sqrt{36-12.96}\) = \(\sqrt{23.04}\) = 4.8 cm
⇒ BC = 2BM = 2 x 4.8 = 9.6 cm
Hence, the distance between Reshma and Mandip = 9.6 cm.
![]()
Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
Let ABC is an equilateral triangle of side 2x metres.
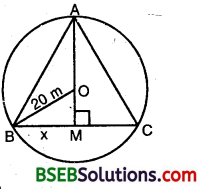
Clearly, BM = \(\frac { BC }{ 2 }\) = \(\frac { 2x }{ 2 }\) = x metres.
In right ∠d ∆ ABM,
AM² = AB² – BM²
= (2x)² – x² = 4x² – x² = 3x²
⇒ AM = \(\sqrt{3} x\)
Now, OM = AM – OA = (\(\sqrt{3} x\) – 20) m
In right ∠d ∆ OEM, we have
OB² = BM² + OM²
⇒ 20² = x² + (\(\sqrt{3} x\) – 20)²
⇒ 400 = x² + 3x² – 40\(\sqrt{3} x\) + 400
⇒ 4x² – 40\(\sqrt{3} x\) =0
⇒ 4x(x – 10\(\sqrt{3}\)) = 0
Since x ≠ 0, ∴ x – 10\(\sqrt{3}\) = 0 ⇒ x = 10\(\sqrt{3}\)
Now, BC = 2BM = 2x = 20\(\sqrt{3}\)
Hence, the length of each string = 20\(\sqrt{3}\) m.