Bihar Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.6 Textbook Questions and Answers.
BSEB Bihar Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.6
![]()
Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given : Two circles with centres A and B, which intersect each other at C and D.
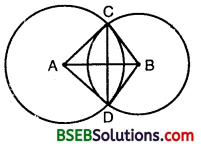
To prove : ∠ACB = ∠ADB
Construction : Join AC, AD, BD and BC.
Proof: In ∆s ACB and ADB, we have
AC = AD [Radii of the same circle]
BC = BD [Radii of the same circle]
∴ By SSS criterion of congruence,
∆ ACB ≅ ∆ ADB
⇒ ∠ACB = ∠ADB [C.P.C.T.]
Question 2.
Two chords AB and CD of length 5 cm and 11 respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of the given circle and let its radius be r cm. Draw OP ⊥ AB and OQ ⊥ CD. Since OP ⊥ AB, OQ ⊥ CD and AB || CD. Therefore, points collinear. So, PQ = 6 cm.

Let OP = x. Then, OQ = (6 – x) cm.
Join OA and OC. Then, OA = OC – r.
Since the perpendicular from the centre to a chord of the circle bisects the chord.
∴ AP = PB = 2.5 cm and CQ = QD = 5.5 cm.
In right ∆s OAP and OCQ, we have
OA² = OP² + AP² and OC² = OQ² + CQ²
⇒ r² = x² + (2.5)² … (1)
and r² = (6 – x)² + (5.5)² … (2)
⇒ x² + (2.5)² = (6 – x)² + (5.5)²
⇒ x² + 6.25 = 36 – 12x + x² + 30.25
⇒ 12x = 60 ⇒ x = 5
Putting x = 5 in (1), we get
r² = 5² + (2.5)2 = 25 + 6.25 = 31.25
⇒ r = \(\sqrt{31.25}\) = 5.6 (approx.)
Hence, the radius of the circle is 5.6 cm (approx.)
![]()
Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre.
Solution:
Let AB and CD be two parallel chords of a circle with centre O such that AB = 6 cm and CD = 8 cm.

Let the radius of the circle be r cm.
Draw OP ± AB and OQ ⊥ CD. Since AB || CD and OP ⊥ AB, OQ ⊥ CD.
Therefore, points O, Q a,nd P are collinear. Clearly OP = 4 cm, and P, Q are mid-points of AB and CD respectively.
AD = PB = \(\frac { 1 }{ 2 }\) AB = 3cm
and, CQ = QD = \(\frac { 1 }{ 2 }\) CD = 4 cm
In rt. ∠D A OAP, we have
OA² = OP² + AP²
⇒ r² = 4² + 3² = 16 + 9 = 25
⇒ r = 5
In rt. ∠D A OCQ, we have
OC² = OQ² + CQ²
⇒ r² = OQ² + 4²
⇒ 25 = OQ² + 16
⇒ OQ² = 9
⇒ OQ = 3
Hence, the distance of chord CD from the centre is 3‘ cm.
Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Since an exterior angle of a triangle is equal to the sum of the interior opposite angles.
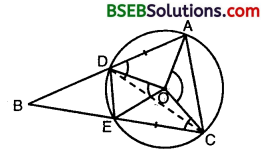
In Δ BDC, we have ∠ADC = ∠DBC + ∠DCB…(1)
Since angle at the centre is twice the angle at a point on the remaining part of circle
Hence, ∠ABC is equal to half the difference of angles subtended by the chords AC and DE at the centre.
![]()
Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given : ABCD is a rhombus.
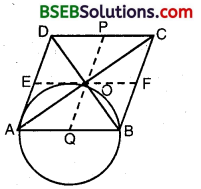
AC and BD are its two diagonals which bisect each other at right angles.
To prove : A circle drawn on AB as diameter will pass through O.
Construction : From O draw PQ || AD and EF || AB.
Proof:
∴ AB = DC ⇒ \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DC
⇒ AQ = DP [∵ Q and P are mid-points of AB and CD]
Similarly AE = OQ
⇒ AQ = OQ = QB
⇒ A circle drawn with Q as centre and radius AQ passes through A, O and B.
The circle thus obtained is the required circle,
Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
In order to prove that AE = AD i.e., A AED is an isosceles triangle it is sufficient to prove that ∠AED = ∠ADE.
Since ABCE is a cyclic quadrilateral.
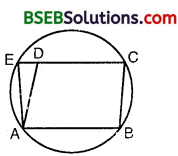
∴ ∠AED + ∠ABC = 180° … (1)
Now, CDE is a straight line.
⇒ ∠ADE + ∠ADC = 180° [∵ ∠ADC and ∠ABC-are opposite angles of a ||gm i.e., ∠ADC = ∠ABC]
From (1) and (2), we get
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∴ In A AED, we have
∠AED = ∠ADE
⇒ AD = AE.
![]()
Question 7.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
Solution:
(i) Let AB and CD be two chords of a circle with center 0.
Let they bisect each other at O.
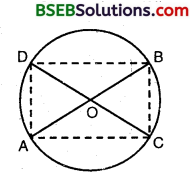
Join AC, BD, AD and BC.
In As AOC and BOD, we have
OA = OB [∵ O is the mid-point of AB]
∠AOC = ∠BOD Wert. opp. ∠s]
and, OC = OD [∵ O is the mid-point of CD]
By SAS criterion of congruence,

⇒ CD divides the circle into two parts
⇒ CD is a diameter.
Similarly, AB is a diameter.
(ii) Since ∆ AOC ≅ ∆ BOD [Prove above]
⇒ ∠OAC i.e., ∠BAC = ∠OBD i.e., ∠ABD
AC || BD
Again, ∆ AOD ≅ ∆ COB
⇒ AD || CB
⇒ ACBD is a cyclic ||gm.
⇒ ∠DAC = ∠DBA … (3) [Opp. ∠s of a ||gm are equal]
Also, ACBD is a cyclic quadrilateral
∴ ∠DAC + ∠DBA = 180°
From (3) and (4), we get
∠DAC = ∠DBA = 90°
Hence, ABCD is a rectangle.
![]()
Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° \(\frac { 1 }{ 2 }\) A, 90° – \(\frac { 1 }{ 2 }\) B and 90° – \(\frac { 1 }{ 2 }\) C.
Solution:
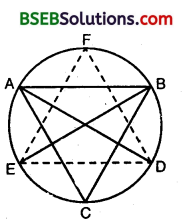
We have ∠D = ∠EDF
= ∠EDA + ∠ADF
= ∠EBA + ∠FCA [∵∠ED A and ∠EBA are the angles in the same Segment of the circle]
∴ ∠EDA = ∠EBA. Similarly, ∠ADF and ∠FCA are the angles in the same segment and hence, ∠ADF = ∠FCA]
= \(\frac { 1 }{ 2 }\)∠B + \(\frac { 1 }{ 2 }\)∠C
[∵ BE is the internal bisector of ∠B and CF is the internal bisector ∠C]
= \(\frac{\angle \mathrm{B}+\angle \mathrm{C}}{2}\)

⇒ The angles of the A DEF are 90° – \(\frac { 1 }{ 2 }\)A, 90° – \(\frac { 1 }{ 2 }\)B and 90° – \(\frac { 1 }{ 2 }\)C.
Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Let O and O’ be the centre of two congruent circles.
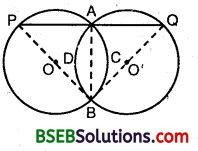
Since AB is a common chqrd of these circles.
∴ arc ACB = arc ADB
⇒ ∠BPA = ∠BQA
⇒ BP = BQ.
![]()
Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Given : ABC is a triangle inscribed in a circle with centre at O. E is a point on the circle such that AE is the internal bisector of ∠BAC and D is the mid-point of BC.
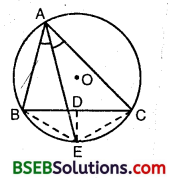
To prove : DE is the right bisector of BC i.e., ∠BDE = ∠CDE = 90°.
Construction : Join BE and EC.
Solution:
In ∆ BDE and ∆ CDE, we have BE = CE
BE = CE
[∵∠BAE = ∠CAE, ∴ arc BE = arc CE ⇒ chord BE = chord CE]
BD = CD [Given]
DE = DE [Common]
∴ By SSS criterion of congruence,
∆ BDE ≅ ∆ CDE
⇒ ∠BDE = ∠CDE [C.P.C.T]
Also, ∠BDE + ∠CDE = 180° [Liner Pair]
∴ ∠BDE = ∠CDE = 90°
Hence, DE is the right bisector of BC.