Bihar Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.3 Textbook Questions and Answers.
BSEB Bihar Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.3
![]()
Question 1.
∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that
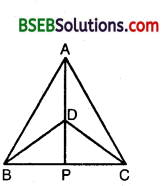
(i) ∆ ABD ≅ ∆ ACD
(ii) ∆ ABP ≅ ∆ ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
Solution:
(i) In ∆s ABD and DBC, we have
AB = AC [Given]
BD = DC [Given]
and, AD = AD [Common]
∴ By SSS criterion of congruence, we have
∆ ABD ≅ ∆ ACD.
(ii) In ∆s ABP and ACP, we have
AB = AC [Given]
∠BAP = ∠PAC
[∵ ∆ ABD = ∆ ACD ⇒ ∠B AD = ∠DAC ⇒ ∠BAP = ∠PAC]
and, AP = AP [Common]
∴ By SAS criterion 6f congruence, we have
∆ ABP ≅ ∆ ACP.
(iii) Since ∆ ABD = ∆ ACD. Therefore,
∠BAD = ∠DAC
⇒ AD bisects ∠A ⇒ AP bisects ∠A … (1)
In ∆s BDP and CDP, we have
BD = CD [Given]
BP = PC [∵ ∆ ASP = ∆ ACP ⇒ BP = PC]
and DP = DP [Common]
∴ By SSS criterion of congruence, we have
∆ BDP ≅ ∆ CDP
⇒ ∠BDP = ∠PDC
⇒ DP bisects ∠D ⇒ AP bisects ∠D … (2)
Combining (1) and (2), we get
AP bisects ∠A as well as ∠D.
(iv) Since AP stands on BC
∴ ∠APB + ∠APC = 180° [Linear Pair]
But ∠APB = ∠APC [Proved above]
∴ ∠APB = ∠APC = \(\frac { 180° }{ 2 }\) = 90°
Also , BP = PC [Proved above]
⇒ AP is perpendicular bisector of BC.
![]()
Question 2.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC, (ii) AD bisects ∠A.
Solution:
AD is the altitude drawn from vertex A of an isosceles ∆ ABC to the opposite base BC so that AB = AC, ∠ADC = ∠ADB = 90°.
Now, in As ADB and ADC, we have
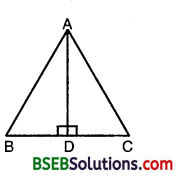
Hyp. AB = Hyp. AC [Given]
AD = AD [Common]
and ∠ADC = ∠ADB [∵ Each = 90°]
∴ By RHS criterion of congruence, we have
∆ ADB ≅ ∆ ADC
⇒ BD = DC and ∠BAC = ∠DAC
[∵ Corresponding parts of congruent triangles are equal]
Hence, AD bisects BC, which proves (i), and AD bisects ∠A, which proves (ii).
Question 3.
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR (see figure). Show that:
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR.
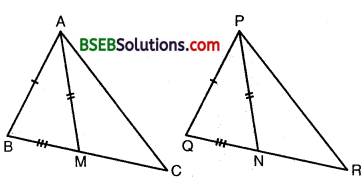
Solution:
Two ∆s ABC and PQR in which AB = PQ, BC = QR and AM = PN.
Since AM and PN are medians of As ABC and PQR respectively.
Now, BC = QR [Given]
⇒ \(\frac { 1 }{ 2 }\)BC = \(\frac { 1 }{ 2 }\)QR ⇒ BM = QN … (1)
Now, in ∆s ABM and PQN, we have
AB = PQ [Given]
BM = QN [From (i)]
and, AM = PN [Given]
∴ By SSS criterion of congruence, we have ∆ ABM = ∆ PQN, which proves (i)
⇒ ∠B = ∠Q … (2)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABC and PQR, we have
AB = PQ [Given]
∠B = ∠Q [From (2)]
BC = QR [Given]
∴ By SAS criterion of congruence, we have
∆ ABC = ∆ PQR, which proves (ii).
![]()
Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
In ∆s BCF and CBE, we have
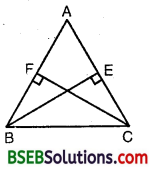
∠BFC = ∠CEB [∵ Each = 90°]
Hyp. BC = Hyp. BC [Common]
FC = EB
∴ By R.H.S. criterion of congruence, we have
∆ BCF ≅ ∆ CBE
⇒ ∠FBC = ∠ECB
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆ ABC
∠ABC = ∠ACB [∵∠FBC = ∠ECB]
⇒ AB = AC [∵ Sides opposite to equal angles of a triangle are equal]
∴ ∆ ABC is an isosceles triangle.
![]()
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:
In ∆s ABP and ACP, we have
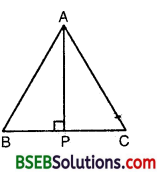
AB = AC [Given]
AP = AP [Common]
and ∠APB = ∠APC [∵ Each = 90°]
∴ By R.H.S. criterion of congruence, we have
∆ ABP ≅ ∆ ACP
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]