Bihar Board 12th Maths Important Questions Long Answer Type Part 5 in Hindi

BSEB Bihar Board 12th Maths Important Questions Long Answer Type Part 5 are the best resource for students which helps in revision.

Bihar Board 12th Maths Important Questions Long Answer Type Part 5 in Hindi

Application of Intregral:

प्रश्न 1.
प्रथम चरण में वृत्त x² + y² = 3², रेखा y = x बा :-अक्ष से घिरे भाय क्षे० ज्ञात करें।
उत्तर:
दिये गये समी०
y = x ……………… (i)
और x² + y² = 3²………………………. (ii)
समी० (i) और (ii) से, वृत्त एवं रेखा का कटान बिन्दु B (4,4) विन्दु B से BM⊥x.
अक्ष पर डाला।
∴ सम्पूर्ण क्षेत्रफल = क्षेत्र OBMO का क्षे० + क्षेत्र BMAB का क्षेत्रफल
अब क्षेत्र OBMO का क्षेत्रफल \(\int_{0}^{4} y d x=\int_{0}^{4} x d x\) ……………..(iii)

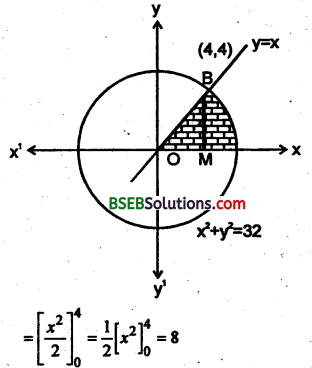
पुनः क्षेत्र BMAB का क्षेत्रफल

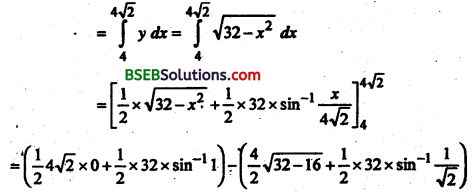
= 8π – (8 + 4π)
= 4π – 8
समी० (i) और (iv) जोड़ने पर,
कुल क्षे० = 8 + 4π – 8 = 4π

प्रश्न 2.
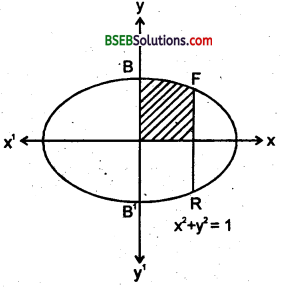
दीर्घवृत्त \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) , x = 0 तथा x = ae से घिरे.भाग का क्षे० ज्ञात करें।
जहाँ b² = a² (1 – e²), e<1.
उत्तर:
दीर्घवृत्त \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) रेखा x = 0 तथा x = ae के द्वारा घिरा भाग BOBRFSB है तो
अब क्षेत्र BOB’RFSB का क्षे०

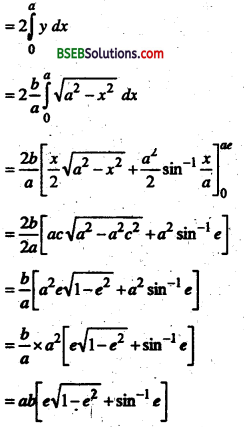
प्रश्न 3.
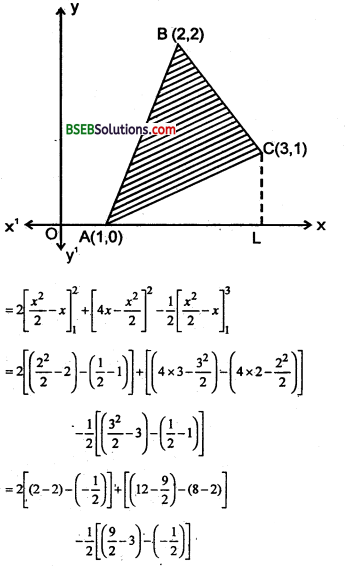
समाकलन के प्रयोग से त्रिभुज ABC का क्षे० ज्ञात करें जिसके शीर्ष क्रमशः A (1,0), B(2,2) तथा C(3, 1) है।
उत्तर:
माना कि ΔABC की शीर्ष A(1,0), B(2,2),C(3, 1) है।
ΔABC का क्षेत्रफल
= ΔABD का क्षे० + समलम्ब चतुर्भुज BDEC का क्षे० – ΔAEC का क्षे०
अब दिये गये AB, BC और CA का समी० क्रमशः
y = 2(x – 1), y = 4 – x,
y = \(\frac { 1 }{ 2 }\) (x – 1)
ΔABC का क्षे० = \(\int_{1}^{2} 2(x-1) d x+\int_{2}^{3}(4-x) d x-\int_{1}^{3} \frac{x-1}{2} d x\)

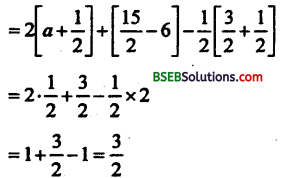
प्रश्न 4.
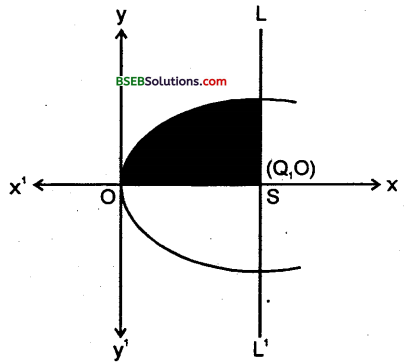
परवलय y² = 4ax एवं नाभिलंब से घिरे भाग का क्षे० ज्ञात करें।
उत्तर:
दिये गये परवलय के समी० y² = 4ax
शीर्ष = (0,0)
नाभिलंब LSL’ का समीकरण x=a
∴ क्षेत्र OLL’O का अभिष्ट क्षे० = 2 (क्षेत्र OLSO का क्षे०)

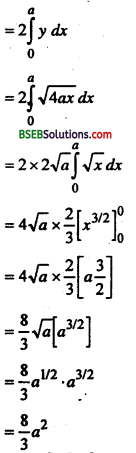
प्रश्न 5.
यदि किसी वक्र का समी० y = a sin (x +b) हो जहाँ a,b constant है तो सका अवकल समी० ज्ञात करें।
उत्तर:
दिया हुआ है,
y = a sin (x + b) ……………(i)
\(\frac{d y}{d x}\) = acos(x + b) ……………(ii)
\(\frac{d^{2} y}{d x^{2}}\) = -asin(x + b) ……………….(iii)
समी० (i), (ii) एवं (iii) से a तथा b का मान विलुप्त करने पर,
\(\frac{d^{2} y}{d x^{2}}\)+ y = 0 ………………….(iv)
जो कि constant a तथा b से स्वतंत्र है। अतः समी० (4) अभीष्ट अवकल समी० हुए।

प्रश्न 6.
निम्न अवकल सपी० \(\frac{d y}{d x}=\frac{x+1}{2-y}\) ( y ≠ 2) का सामान्य जाति करें।
उत्तर:
दिया हुआ है,
\(\frac{d y}{d x}=\frac{x+1}{2-y}\) ………………. (i)
समी० (i) में चर को अलग करने पर हम पाते हैं
∫(2 – y) dy = ∫(x + 1) dx
समी० (2) को दोनों तरफ समाकलन करने पर हम पाते हैं
∫(2 -y) dy = ∫(x + 1) dx
या, 2y – \(\frac{y^{2}}{2}=\frac{x^{2}}{2}\) + x + c₁
या, x² + y + 2x – 4y + 2c₁ = 0
x² + y² + 2x – 4y + c = 0 जहाँ c = 2c
जो समी० (1) का सामान्य हल है।

प्रश्न 7.
समीo \(\frac{d y}{d x}\) = – 4xy² दिया हुआ है y = I; जहाँ x = 0 का Particular हल ज्ञात करें।
उत्तर:
यदि y ≠ 0, तो दिये गये अवकल समी० निम्न
\(\frac{d y}{y^{2}}\) = -4x dx
\(\int \frac{d y}{y^{2}}\) = -4∫xdx या, \(-\frac{1}{y}\) = -2x² + c
या, y = \(\frac{1}{2 x^{2}-c}\)
4x dr.
जबःy = 1 तथा x = 0 हो तो समी० (ii) से, c = -1
समी० (2) में c का मान रखने पर,
y = \(\frac{1}{2 x^{2}+1}\)

प्रश्न 8.
एक बैंक में मूलधन एक सतत दर 5% प्रतिवर्ष की दर से बढ़ रहा है तो कितने वर्षों में 1000 रु० अपने आप का दुगुना हो जायेगा।
उत्तर:
माना कि किसी समय t पर मूलधन p है, तो

p= 1000 . जब t = 0
Pऔर t का मान समी० (3) पर रखने पर
हम पाते हैं c = 1000
∴ समीकरण (iii) से पाते हैं
p = 1000^t/20
माना कि t समय में मूलधन दुगुना हो जाता है
2000 = 100^t/20
t = 20log_e²

प्रश्न 9.
सिद्ध करें कि समी० x – y \(\frac{d y}{d x}\) = x + 2y समघातीय अवकल समी० है
उत्तर:
\(\frac{d y}{d x}=\frac{x+2 y}{x-2 y}\)
माना F(x,y) = \(\frac{x+2 y}{x-y}\)
अब . F(λx,λy)
= \(\frac{\lambda(x+2 y)}{\lambda(x-y)}\) λ⁰ = f(x,y)
∴ F (x, y), शून्य घात का समघातीय संमी० है।

प्रश्न 10.
सिद्ध करें कि समी० xcos\(\left(\frac{y}{d x}\right) \frac{d y}{d x}=y \cos \left(\frac{y}{x}\right)\) + x समघातीय समी० है। एवं इसे हल करें।
उत्तर:

f(x, y) समघातीय अवकल समी० है।
y = vx रखने पर
समी० (i) को अवकलित करने पर,

या, sin v= log |x| + loge
या, sin v = log |ex|
v = \(\frac { y }{ x }\) रखने पर
sin (y/x) = log|ex|

प्रश्न 11.
समी० x\(\frac{d y}{d x}\) + 2y = x² (x ≠ 0) का General Soln ज्ञात करें \
उत्तर:
दिया गया अवकल समी०
x\(\frac{d y}{d x}\) + 2y = x² ………………….. (i)
दोनों ओर x से भाग देने पर
\(\frac{d y}{d x}+\frac{2}{x} y=x\) ……………………(ii)
जो कि \(\frac{d y}{d x}\) + py = Q , के रूप का linear dift. समी० है।

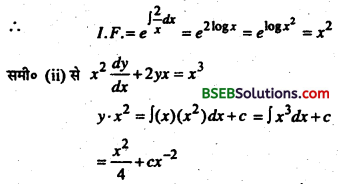
जो कि दिये गये आकलन समी० का सामान्य समी० है।

प्रश्न 12
अवकल समी० (x +2y²)dy = ydx का general soln. ज्ञात करें।.
उत्तर:
दिया गया समी० (x+2y²) dy = ydx
\(\frac{d x}{d y}-\frac{x}{y}=2 y\) ………………. (i)
जो कि \(\frac{d x}{d y}\) + p₁x = Q₁ के रूप का linear dift. समी० है।
जहाँ P₁ = \(-\frac{1}{y}\)
और Q₁ = 2y
∴ I.F = \(e^{\int-\frac{1}{y} d y}=e^{-\log y}=e^{\log (y)^{-1}}=\frac{1}{y}\)
समी० (i) में दोनों ओर I.F. से गुणा करने पर
\(\frac{1}{y} \cdot \frac{d x}{d y}-\frac{x}{y^{2}} \) = 2
x. \(\frac{1}{y}\) = ∫2dy \(\frac{1}{y}\)dy + c
या, \(\frac{x}{y}\) = ∫2dy + c
या, \(\frac{x}{y}\) = 2y + c
या, x = 2y² + cy
जो कि अभीष्ट General समी० हुए।

प्रश्न 13.
अवकल समी० (tan^-1y – x) dy = (1 + y²) dx को हल करें।
उत्तर:
दिये गये अवकल समी०
\(\frac{d x}{d y}+\frac{x}{1+y^{2}}=\frac{\tan ^{-1} y}{1+y^{2}}\) ………………… (i)
समी० (i) \(\frac{d x}{d y}\) + P₁x = Q₁ के रूप का Linear Diff. cqn. है।

tan^-1 = t रखने पर
∴ \(\frac{1}{1+y^{2}}\) dy = dt
I = ∫ te^tdt
= te^t – ∫ 1. e^t dt
= te^t – e¹
= e^t (t – 1)
I = e^tan-1y (tan^-1 y – 1)
समी० (ii) से
x.etan^-1y = e^tan-1y (tan^-1y – 1) + c
या, x= (tan^-1y – 1) + c.e ^tan-1y
जो कि अभीष्ट General soln. है।

प्रश्न 14.
वृत्त x² + y² = a² का क्षे० ज्ञात करें।
उत्तर:
पूर्ण वृत्त का क्षेत्र –
4 . (area of region AOBA
= \(4 \int_{0}^{d} y d x\)
= \(4 \int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\)
∵ क्षेत्र AOBA, प्रथम चरण में स्थिर है। .
∴ y = +ve

अवकल समीकरण

प्रश्न 1.
हल करें : x cos (y/x) (ydx + xdy) = y sin(y/x) (xdy – ydx).
उत्तर:
माना कि y = vx ⇒ dy = vdx + xdv. अतः दत्त समीकरण से,
xcos v(vxdx + vxdx + x² dv) = vxsin (vxdx + x²dv – vxdx)
cosv(2vxdx + x² dv) = vsin v x x² dv
xcos v(2vdx+xdv) = x² vsin v dv
2vdx + xdv = vx tan v dv.
2\(\frac{d x}{x}+\frac{d v}{v}\) = tan v dv.
Integrate करने पर,
2logx + logy = log sec v + logk
vx² cosv = k ⇒ xy cos(y/x) = k

प्रश्न 2.
हल करें : (1 + y²)dx = (tan^-1y – x).dy
उत्तर:

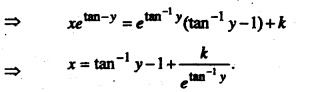
प्रश्न 3.
हल करें (x + y²)\(\frac{d y}{d x}\) = a²
उत्तर:
a² \(\frac{d x}{d y}\) = (x + y)²
माना कि x + y = z ⇒ \(\frac{d x}{d y}+1=\frac{d z}{d y}\)
⇒ \(\frac{d x}{d y}=\frac{d z}{d y}\) – 1 अतः (1) से

प्रश्न 4.
सिद्ध करें कि समपातीय अवकलन के समीकरण x.dy – y. dx = \(\sqrt{x^{2}+y^{2}}\) होंगे तथा हल करें।
उत्तर:
दिये गये समीकरण

∴ f(x) समघातीय अवकलन के समीकरण है सिद्ध हुआ।
\(\frac { y }{ x }\) = v रखने पर
y = vx
∴ \(\frac{d y}{d x}=v+x \cdot \frac{d v}{d x}\)
समीकरण (i) से,

प्रश्न 5.
हल करें : x\(\frac{d y}{d x}\) = y(logy – logx – 1)
उत्तर:
दिया गया समीकरण
x\(\frac{d y}{d x}\) = y(logy – logx – 1)
\(\frac{d y}{d x}=\frac{y}{x}\) (logy – logx – 1) …..(i)
v = \(\frac { y }{ x }\) रखने पर
y = vx
∴ \(\frac{d y}{d x}=v+x \cdot \frac{d v}{d x}\)
समीकरण (i) से,
v + x.\(\frac{d v}{d x}\) = v(logv – 1)

बायाँ पक्ष के लिए,
logv – 2 = t रखने पर
: 1/v dv = dt
समीकरण (ii) से,
\(\int \frac{d t}{t}=\int \frac{d x}{x}\)
log|t| = log |x| + log |c|
= log|t| = log|x| . c
|t| = |x| .c
\(\left|\log \left(\frac{y}{x}\right)-2\right|=|x| c\)
|logy-logx- 2| = c|x|

प्रश्न 6.
हल करें:
\(\frac{d y}{d x}\) + 2y = sin x
उत्तर:
दिया गया समीकरणं
\(\frac{d y}{d x}\) + 2y = sin x
माना I.F. = e^∫2dx = e^2x
समीकरण (i) से,

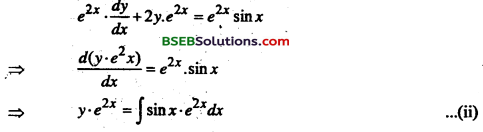
प्रश्न 7.
हल करें: (x² – 1) \(\frac{d y}{d x}\) + 2xy = \(\frac{2}{x^{2}-1}\)
उत्तर:
दिया गया समीकरणं

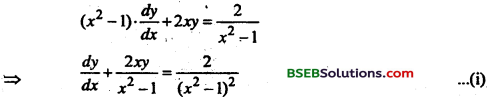
माना कि I.F = e\(\int \frac{2 x}{x^{2}-1} d x\)
माना कि x² – 1 = t
∴ 2x. dx = dt

प्रश्न 8.
हल करें : \(\frac{d y}{d x}\) – 3ycotx = sinx
दिया हुआ है :y= 2, जब x = \(\frac{\pi}{2}\)
उत्तर:
दिया हुआ समीकरण
\(\frac{d y}{d x}\) – (3cotx).y = sin2x
-∫(3cotx).dx-3logsinx
माना I.F = e^{-∫(3cot x)dx} = e^{-3log sin x}

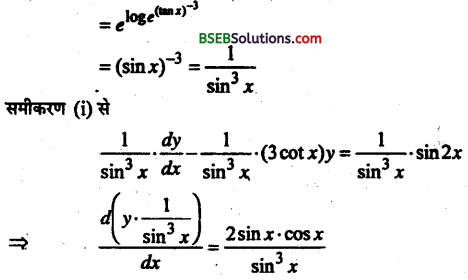
⇒ \(y \cdot \frac{1}{\sin ^{3} x}=\int \frac{2 \cos x}{\sin ^{2} x} \cdot d x\)
माना कि sinx = t
∴ Cosx.dx = dt

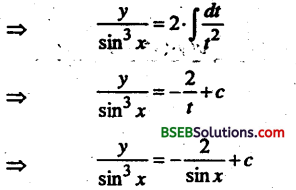
y = -2 sin²x + c sin³x
x = \(\frac{\pi}{2}\), y = 2 पर
2 = -2sin²\(\frac{\pi}{2}\) + csin³\(\frac{\pi}{2}\)
2 = -2 + c
c = 4.
समीकरण (ii) से
y = -2sin²x + 4sin³x

प्रश्न 9.
हल करें :
\(\frac{d y}{d x}+\frac{1}{x}=\frac{e^{y}}{x}\)
उत्तर:
दिया गया समीकरण

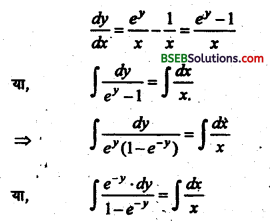
माना किं 1 – e^-y = t
∴ e^-y dy = dt
या \(\int \frac{d t}{t}=\int \frac{d x}{x}\)
log|t| = log |x| + logc
= log|1-e^-y|= log(|x|.c)
1 – e^-y = c|x|

प्रश्न 10.
इल करें :
\(\frac{d^{2} y}{d x^{2}}\) = sec² x + x.e^x
उत्तर:
x के सन्दर्भ में दोनों तरफ समाकलन करने पर

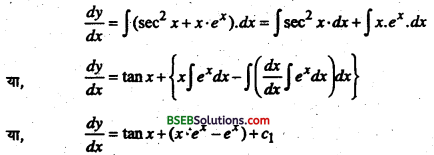
पुनः x के सन्दर्भ में समाकलन करने पर।
y = ∫tan x.dx + ∫x.e^x.dx – ∫e^x dx + c ∫ dx
या y = log |secx| + (xe^x – e^x) – e^x + c₁ x + c₂
y = log |secx| + xe^x + c₁ x + c₂

प्रश्न 11.
हल करें :
xdy + ydx = xe^xdx
उत्तर:
दिया गया समीकरण
xdy + y dx = xe^x dx
या x dy = (xe^x – y)dx
या x.\(\frac{d y}{d x}\) = xe^x – y
या x.\(\frac{d y}{d x} x\) + y = xe^x
या \(\frac{d y}{d x}+\frac{y}{x}\) = e^x
माना I.F = \(e^{\int \frac{1}{x} d x}=e^{\log _{e}^{x}}\) = x
समीकरण (i) से,
\(x \cdot \frac{d y}{d x}\) = y = x .e^x
या \(\frac{d(x \cdot y)}{d x}\) = x .e^x
या y.x = ∫ e^x. x. x . dx
या y.x = ∫e^x dx – ∫ \(\left(\frac{d x}{d x} \cdot \int e^{x} \cdot d x\right) d x\)
या y.x = x.e^x – e^x + c

प्रश्न 12.
हल करें :
(x +2y³) \(\frac{d y}{d x}\) = y.
उत्तर:
दिया गया समीकरण
(x + 2y³ \(\frac{d y}{d x}\) = y
था, x + 2y³ = y. \(\frac{d x}{d y}\)
था, y\(\frac{d x}{d y}\) – x = 2y³

या \(\frac{x}{y}\) = ∫2ydy
या \(\frac{x}{y}\) = \(\frac{2 y^{2}}{2}\) + c
या \(\frac{x}{y}\) = y² + c
या x = y³ + cy

प्रश्न 13.
\(\frac{d y}{d x}\) + y cot x = 2y² cos x
उत्तर:
\(\frac{1}{y^{2}} \frac{d y}{d x}+\frac{1}{y} \cot x=2 \cos x\) …………….(1)
Put 1/y = z ⇒ \(\frac{1}{y^{2}} \frac{d y}{d x}=\frac{-d z}{d x}\)
∴ (1) \(-\frac{d z}{d x}\) + zcotx = 2cos x
\(\frac{d z}{d x}\) – zcotx = -2cos x ………….(2)

∴ I:F. = e^-∫cotxdx = e^{-logsin x} = cosecx
Multiplying (2) by IF and integrating, we have
zx cosec x = -∫cosx.cosec xdx = – 2∫cotx
z cosec x = -2 log sin x + k
\(\frac{cosec x}{y}\) = -2logsin x+k

प्रश्न 14.
\(\frac{d y}{d x}\) + y secx = tan x
Anss.
I.F. = e∫sec x dx = e^{∫log(sec + tanx)} = sec x + tan x.
Multiplying the given eqn. with 1.F.and integrating we get
∴ y x (sec x + tan x) = ∫tan x(secx + tan x) dx
= ∫tanx secx dx + (sec² x – 1)dx .
= y(secx + tan x) = sec x + tan x – x + k

प्रश्न 15.
मान निकालें ∫ sec³ x dx
उत्तर:
I = [sec³ x dx = sec² x.sec xdx
I = sec x∫ sec² x dx – ∫ [\(\frac{d}{d x}\)(sec x) ∫sec² xdx]dx
= sec x tanx – ∫ secx . tan x tan x dx
= sec x tan x – ∫ secx(sec² x – 1)dx
= secx tan x – ∫ sec³ xdx + ∫ secxdx
= sec x tan x – I + log(secx + tanx) +k
2I = sec x . tan x + log (secx + tan x) +k
I = \(\frac { 1 }{ 2 }\) secx tan x + \(\frac { 1 }{ 2 }\)log(secx + tanx) + c

प्रश्न 16.
मान निकालें ∫ cos \(\sqrt{x}\) dx
उत्तर:
Let \(\sqrt{x}\) = z
x = z² ⇒ dx = 2zdz
∴ I = ∫ cos z. 2zdz = 2 ∫ z cos z dz
= 2z∫ cos z dz – 2 ∫[\(\frac{d}{dz}\)(z) ∫ cos zdz]dz
= 2z sinz – 2∫sin zdz
= 2 z sinz + 2 cos z + c
I = \(2 \sqrt{x} \sin \sqrt{x}+2 \cos \sqrt{x}+c\)