Bihar Board 12th Maths Important Questions Long Answer Type Part 6 in Hindi

BSEB Bihar Board 12th Maths Important Questions Long Answer Type Part 6 are the best resource for students which helps in revision.

Bihar Board 12th Maths Important Questions Long Answer Type Part 6

Vector Algebra

प्रश्न 1.
कोई तीन सदिरा \(\vec{a}\), \(\vec{b}\) और के लिए
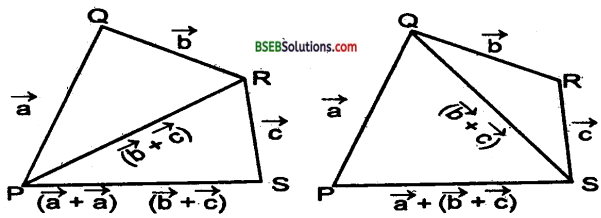
(\(\vec{a}\) + \(\vec{b}\)) + \(\vec{c}\) = \(\vec{a}\) + (\(\vec{b}\) + \(\vec{c}\)).
उत्तर:

त्रिविमिय ज्यामिति

प्रश्न 2.
रेखा के सदिश समी० एवं कार्तीय समीकरण ज्ञात करें जो बिन्दु (5,2,-4) से होकर गुजरता है तथा सदिश 3î + 2j ̂ – 8k̂ के समानान्तर है।
उत्तर:
दिया गया है – \(\vec{a}\) = 5î + 2ĵ – 4k̂ तथा \(\vec{b}\) = 3î + 2j ̂ – 8k̂
इसलिए रेखा का सदिश समी०- .
\(\vec{r}\) = 5î + 2ĵ – 4k̂ + λ(3î + 2j ̂ – 8k̂)
अब, \(\vec{r}\) कोई बिन्दु P (x, y, z) पर स्थिति संदिश है।
इसलिए xî + yĵ + 2k̂ = 5î + 2ĵ – 4k̂ + λ(3î + 2j ̂ – 8k̂)
= (5 + 3λ)î + (2 + 2λ)ĵ + (- 4 – 8λ)k̂
λ को हटाने पर हम पाते हैं कि,
\(\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}\)
अत: यह समीकरण रेखा के कार्तीय रूप में है।

प्रश्न 3.
रेखा के जोड़ा के बीच का कोण ज्ञात करें जो दिया गया है-…
\(\vec{r}\) = 3î + 2ĵ – 4k̂ + λ(î + 2ĵ + 2k̂)
तथा \(\vec{r}\) = 5î – 2ĵ + μ(3î + 2ĵ + 6k̂)
उत्तर:
यहाँ \(\overrightarrow{b}_{1}\) = î + 2ĵ + 2k̂ तथा \(\overrightarrow{b}_{2}\) = 3î + 2ĵ + 6k̂ दो रेखा के बीच का कोण θ दिया गया है तो

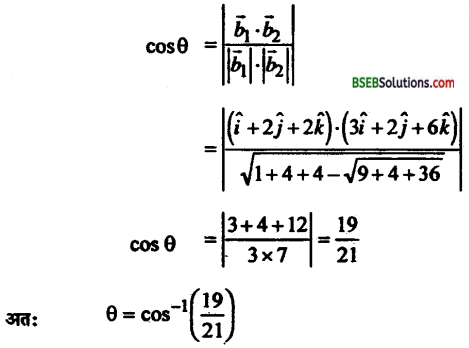
प्रश्न 4.
रेखा l₁ तथा l₂ के बीच न्यूनतम दूरी ज्ञात करें जिसकी सदिश समीकरण है –
\(\vec{r}\) = î + ĵ + λ(2î – ĵ + k̂ ) ….. (i)
तथा. \(\vec{r}\) = 2î + ĵ – \(\vec{k}\) + μ(3î + 5ĵ + 2\(\vec{r}\)) …… (ii)
उत्तर:
समीकरण (i) तथा (ii) से \(\vec{r}=\vec{a}_{1}+\lambda \vec{b}_{1}\) तथा \(\vec{r}=\vec{a}_{2}+\mu \vec{b}_{1}\) का तुलना करने पर क्रमशः हम पाते हैं
\(\vec{a}_{1}\) = î + ĵ, \(\vec{b}_{1}\) = 2î – ĵ + k̂
\(\vec{a}_{2}\) = 2î + ĵ – k̂ तथा \(\vec{b}_{2}\) = 3î – 5ĵ + 2k̂
इसलिए \(\vec{a}_{2}\) – \(\vec{a}_{1}\) = î – k̂
तथा \(\vec{b}_{1} \times \vec{b}_{2}\) = (2î – ĵ + k̂) × (3 – 5ĵ + 2k̂)

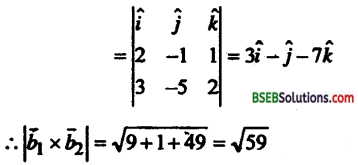
अतः दिया गया रेखा के बीच के न्यूनत्तम दूरी

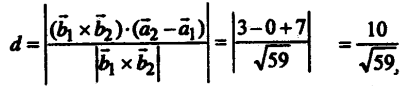
प्रश्न 5.
सतह के सदिश समीकरण ज्ञात करें जो सतह \(\vec{r}\)(î + ĵ + k̂) = 6 तथा । \(\vec{r}\)(2î + 3ĵ + 4k̂) = – 5 के कटान तथा बिन्दु (1, 1, 1) से होकर गुजरता है।
उत्तर:
यहाँ \(\vec{n}_{1}\) = î + ĵ + k̂ तथा \(\vec{n}_{2}\) = 2î + 3ĵ + 4k̂
तथा d₁ = 6 तथा d₂ = – 5
अतः सम्बन्ध \(\vec{r}\left(\vec{n}_{1}+\lambda \vec{n}_{2}\right)\) = d₁ + λd₂ का उपयोग करने पर हम लोग पाते हैं-
\(\vec{r}\) ∙ [î + ĵ + \(\vec{k}\) + λ(2î + 3ĵ + 4\(\vec{k}\)] = 6 – 5λ
\(\vec{r}\) [(j + 2λ)î + (1 + 3λ)j + (1 + 4λk̂] – 6 – 5λ …. (i)

जहाँ λ कुछ वास्तविक संख्या है
\(\vec{r}\) = xî + yĵ + 2k̂; लेने पर हम पाते हैं कि
(xî + yĵ + 2k̂) (1 + 2λ)î + (1 + 3λ)ĵ + (1 + 4λ)k̂] = 6 – 5λ
या, (1 + 2λ)x + (1 + 3λ)y + (1 + 4λ)z = 6 – 5λ
या, (x + y + z – 6) + λ(2x + 3y + 4z + 5) = 0 ……. (iii)
दिया गया सतह जो बिन्दु (1, 1, 1) से होकर गुजरता है अवश्य ही समीकरण (ii) को संतुष्ट करेगा। अर्थात्
(1 + 1 + 1 – 5) + λ (2 + 3 + 4 + 5) = 0
या, λ = \(\frac{3}{14}\)
λ का मान समीकरण (i) में रखने पर हम पाते हैं

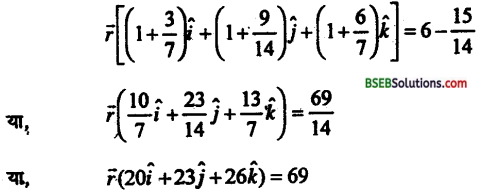
जो सतह सदिश का प्राप्त समीकरण है।

प्रश्न 6.
सदिश तरीका का उपयोग कर 2x + y – 2x = 5 तथा 3x -6y – 2x = 7 दो सतहों के बीच का कोण ज्ञात करें।
उत्तर:
दो सतहों के बीच का कोण उन सतहों के अभिलम्बों के बीच का कोण होता है। प्रशन से दिये गये सतह के समी० से माना कि
\(\vec{N}_{1}\) = 2î + ĵ – 2k̂ तथा \(\vec{N}_{2}\) = 3î – 6ĵ – 2k̂
इसलिए,

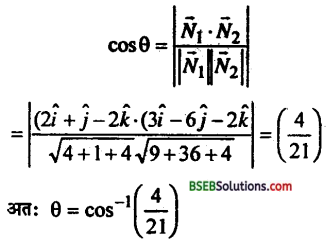
प्रश्न 7.
सदिश 3\(\vec{i}\) + 2\(\vec{j}\) – 6\(\vec{k}\) तथा 4\(\vec{i}\) – 3\(\vec{j}\) – \(\vec{k}\) के बीच का कोण निकालें।
उत्तर:
हल : मान लिया कि प्रदत्त सदिशों के बीच का कोण θ है।

प्रश्न 8.
सदिश \(\vec{a}=2 \vec{i}-3 \vec{j}+\vec{k}, \vec{b}=3 \vec{i}-\vec{j}-2 \vec{k}\) के बीच के कोण की ज्या निकालें।
उत्तर:

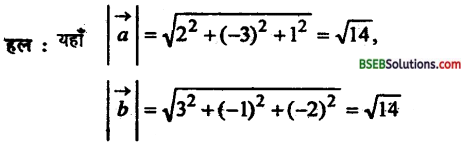
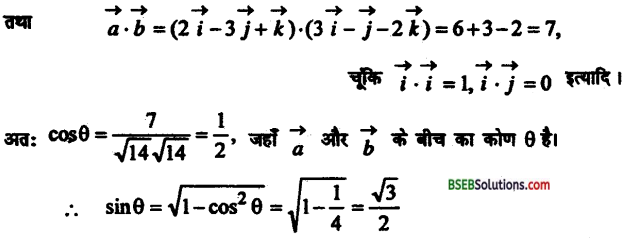
प्रश्न 9.
सदिश \(3 \vec{i}+\vec{j}+2 \vec{k}\) और \(2 \vec{i}-2 \vec{j}+4 \vec{k}\) के बीच के कोण की ज्या निकालें।
उत्तर:
हल : मान लिया कि

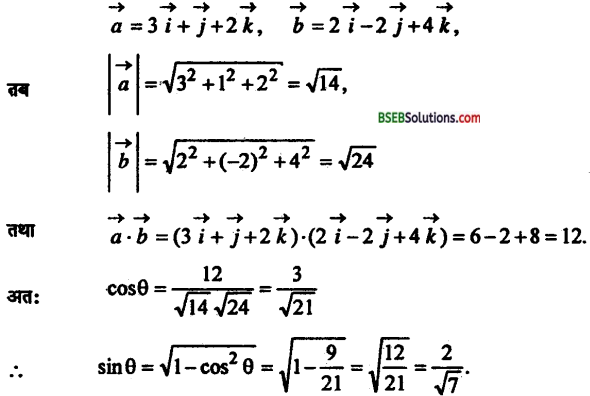
प्रश्न 10.
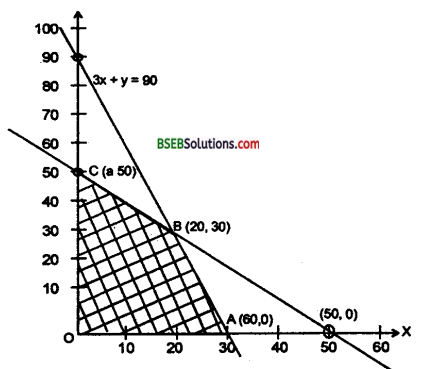
यदि \(|\vec{a}+\vec{b}|=|\vec{a}-\vec{B}|\) तो सिद्ध करें कि \(\vec{a}\), \(\vec{b}\) परस्पर लम्ब हैं।
उत्तर:

प्रश्न 11.
रेखा 10x + 2y – 11z = 3 तथा तल \(\frac{x+1}{2}=\frac{y}{3}=\frac{z-3}{6}\) के बीच का को जात करेंगे।
Ans.
माना कि रेखा तथा सतह के बीच का कोण 8 है। दिया गया समीकरण को सदिश रूप में बदलने पर हम पाते हैं कि
\(\vec{r}\) = (-î + 3k̂) + λ(2î + 3ĵ + 6k̂).
तथा \(\vec{r}\) (10î + 2ĵ – 11k̂) = 3
यहाँ \(\vec{b}\) = 2î + 3ĵ + 6k̂
तथा \(\vec{n}\) = 10î + 2ĵ – 11k̂

प्रश्न 12.
सतह का समीकरण ज्ञात करें जिसका बिन्दु (1, -1, 2) तथा प्रत्येक सता 2x + 3y – 2z = 5 तथा x + 2y – 3z = 8 पर लम्ब है।
उत्तर:
सतह का समीकरण जिसका बिन्दु दिया गया है
A(x – 1) + B(y + 1) + C(z – 2) = 0 ………… (i)
समीकरण (i) में सतह के साथ लम्बात्मक का शर्त लागू करने पर :
2x + 3y – 2x = 5 तथा x + 2y – 3x = 8
हमलोग पाते हैं कि
2A + 3B – 2C = 0 तथा A + 28 – 3C = 0
इस समीकरण को हल करने पर हम पाते हैं
A = 5C तथा B = 4C
अतः प्राप्त समीकरण -5C(x – 1) + 4C(y + 1) + C(z – 2) = 0 है।
अर्थात् 5x – 4y – z = 7

प्रश्न 13.
बिन्दु का नियामक ज्ञात करें जहाँ रेखा बिन्दु A (3, 4, 1) तथा B (5, 1, 6) से होकर गुजरता है और XY सतह को पार करता है।
उत्तर:
रेखा का सदिश समीकरण जो बिन्दु A तथा B से होकर गुजरता है।
\(\vec{r}\) = 3î + 4ĵ + k̂ + λ [(5 – 3)î + (1 – 4)ĵ + (6 – 1)k̂]
अर्थात् \(\vec{r}\) = 3î + 4ĵ + k̂ + λ(2î – 3ĵ + 5k̂)
माना कि P एक विन्दु है जब रेखा xy सतह के पार करता है तब विन्दु p का स्थिति सदिश xî + yĵ के रूप में है।
तब बिन्दु अवश्य ही समीकरण (i) को संतुष्ट करेगा।
अर्थात् xî + yĵ = (3 + 2λ)î +(4 – 3λ)ĵ + (1 + 5λ)k̂.
î तथा ĵ के गुणांक को समान करने पर हमलोग के पास है,
x = 3 + 2λ.
y = 4 – 3λ
0 = 1 + 5λ
ऊपर के समीकरण को हल करने पर हम पाते हैं –
x = \(\frac{13}{5}\) तथा y = \(\frac{23}{5}\)
अतः बिन्दु का प्राप्त नियामक (\(\frac{13}{5}\), \(\frac{23}{5}\), 0) है।

प्रश्न 14.
सतह 2x – 3y + 4z – 6 = 0 से मूल बिन्दु के बीच की दूरी ज्ञात करें।
उत्तर:
∵ तल के अभिलंब का दिक् अनुपात 2,-3 तथा 4 है।
∴ तल के दिक् कोज्या

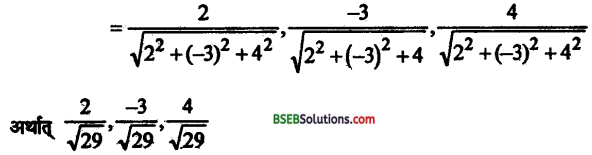
अतः समीकरण 2x – 3y + 4z – 6 = 0 को विभाजित करने पर
अर्थात् x – 3y + 4z = 6 को √29 के द्वारा हम पाते हैं
\(\frac{2}{\sqrt{29} x}+\frac{-3}{\sqrt{29}} y+\frac{4}{\sqrt{29}} z=\frac{6}{\sqrt{29}}\)
यह lx + my + nz = d का रूप है जहाँ d मूल बिन्दु से सतह की दूरी है। इसलिए मूल
बिन्दु से सतह की दूरी \(\frac{6}{\sqrt{29}}\) है

प्रश्न 15.
एक घन के विकर्ण के साथ एक रेखा α, β, γ तथा δ कोण बनाता है तो सिद्ध करें कि cos²α + cos²β + cos²γ + cos²δ = \(\frac{4}{3}\)
उत्तर:
माना कि एक आयताकार घन है जिसकी लम्बाई चौड़ाई तथा ऊंचाई समान है। माना OADBFEGC एक घन है जिसकी प्रत्येक भुजा की लम्बाई a इकाई है।

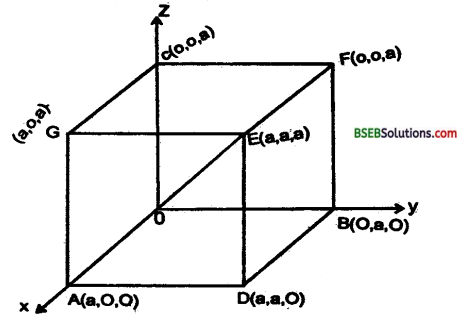
जिसकी 4 विकर्ण OE, A F BG तथा CD है।
विकर्ण OE का Direction cosines जो रेखा दो बिन्दु O तथा E. को जोड़ता है।

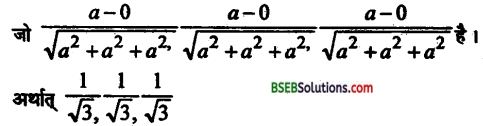
इस प्रकार Direction cosines AF, BG तथा CD के साथ क्रमशः

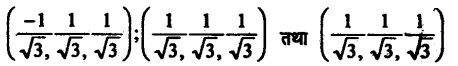
माना कि.l, m, n दिया गया रेखा का Direction cosines है जो OE, AF, BG, CD के साथ क्रमशः α, β, γ, δ कोण बनाता है।
तब cos α = \(\frac{1}{\sqrt{3}}\) (l + m + n)
cos β = \(\frac{1}{\sqrt{3}}\) (- l + m + n)
cos γ = \(\frac{1}{\sqrt{3}}\) (l – m + n)
cos δ = \(\frac{1}{\sqrt{3}}\) (l + m – n)
वर्ग करके जोड़ने पर हम पाते हैं कि
cos²α + cos²β + cos²γ + cos²δ
= \(\frac{1}{3}\)[(l + m + n)² + (- l + m + n) + (l – m + n)² + (l + m – n)²]
= \(\frac{1}{3}\) [4(l² + m² + n²) = (जैसे – l² + m² + n² = 1)

प्रश्न 16.
नीचे दिये गये Programming को Solve करें ।
उत्तर:
graphically maximise z = 4x + y ….(i)
Subject to the constraints-
x + y ≤ 50 ….(ii)
3x + y ≤ 90 …. (iii)
x ≥ 20, y ≥ 20 ….(iv)
उत्तर:
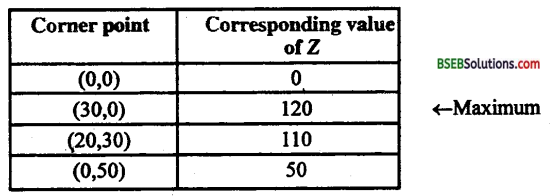
चित्र में छायांकित भाग किये गये Constraints (ii), (iii), (iv) के अनुसार है। Co-ordinates of corner points
o = (0, 0), A = (30, 0), B = (20, 30) C = (0, 50)


∴ Maximum value of Z = 120 at (30, 0)

प्रश्न 17.
एक dietician दो प्रकार के Foodsp and each pocket containing 30g) का प्रयोग करता है । Food p में 12 Units, Calcium, 4 Units Iron,6Units कोलेस्ट्रॉल तथा 6 Units विटामिन A है । Food Q वाले प्रत्येक थैले में 3 Units कैल्शियम, 20 Units आयरन, 4Units कोलेस्ट्रॉल तथा 3 Units Vitamin A एक पूर्ण Diet में कम से कम 240 Units कैल्शियम, कम से कम 460 Units आयरन तथा अधिक से अधिक 300 Units कोलेस्ट्रॉल जरूरी है। तो कम से कम विटामिन A होने के लिए प्रत्येक प्रकार के Food के Pockets कितना उपयोग किया जाय ? एवं विटामिन Aका Minimum amount क्या होगा?
उत्तर:
माना कि Pockets P की संख्या x तथा Pockets q की संख्या y है।
∴ x ≥ 20, y ≥ 20
(Vitamin A)
z = 6x + 3y Subject to the constraints.
12x + 3y ≥ 240 (Calcium)
या, 4x + y ≥ 80              …. (i)
4x + 20y ≥ 460 (iron)
या,. x + 5y ≥ 115             …… (ii)
6x + 4y ≤ 300 (Cholesterol)
या, 3x + 2y ≤ 150
x ≥ 0, y ≥ 0 ….. (iv)
समी. (i), (ii), (iii) एवं (iv) से, ग्राफ खींचने पर।

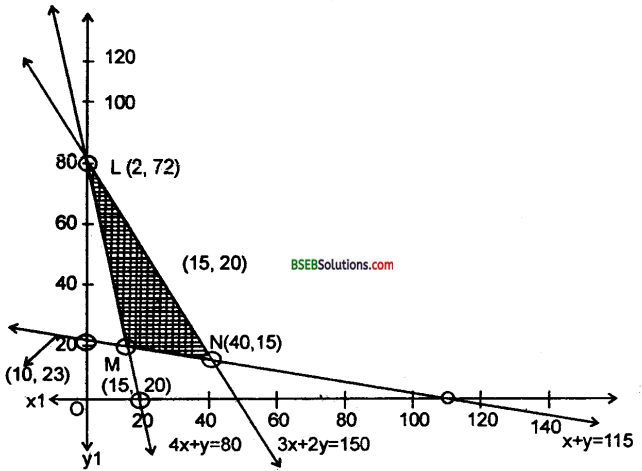
Co-oridnotes of corner points L = (2, 72)
M = (15, 20), N = (40, 15).

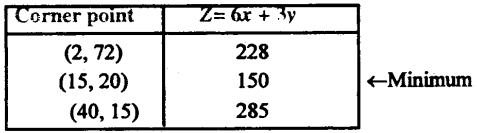
∴ Z is minimum of the point (15, 20).
अतः दिये गये प्रतिबंध के अंतर्गत विटामिन A minimum होगा यदि 15 packets food p तथा 20 packets food Q उपयोग किये जाएं एवं विटामिन का उपयोग किया गया . minimum amount = 150 units.

प्रश्न 18.
एक Box में दस कार्ड हैं जिस पर 1 से 10 तक अंकित है जिन्हें आपस में मिलाने के बाद एक कार्ड खींचा गया है। यदि यह ज्ञात हो कि खींचे गये कार्ड पर 3 से अधिक अंकित हैं तो उसके सम संख्या होने की प्रायिकता ज्ञात करें।
उत्तर:
माना कि A = एक कार्ड पर सम संख्या होने की घटना है
तथा B = एक कार्ड पर 3 से अधिक होने की घटना है तो P(A/B) = ?
∴ प्रयोग का Sample Space (S) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {2, 4, 6, 8, 10} B = {4, 5, 6, 7, 8, 9, 10}
∴ A ∩ B = {2, 4, 6, 8, 10} ∩ {4, 5, 6, 7, 8, 9, 10}
= {4, 6, 8, 10}

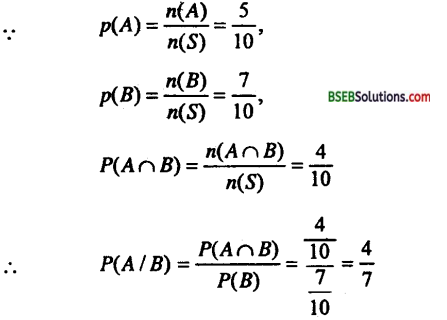
प्रश्न 19.
एक पासे के तीन उछाल में घटना A और B निम्न प्रकार है:
A → तीसरे उछाल में 4 होना। …
B → प्रथम उछाल में 6 तथा द्वितीय उछाल में 5 होना तो B के घटित हाने पर घटना 4 के होने की प्रायिकता ज्ञात करें।
उत्तर:
n (5) = 6 × 6 × 6 = 216
A = { (1, 1, 4), (1, 2, 4),……., (1, 6, 4),(2, 1, 4), (2,2,4),…….,
(2, 6, 4), (3, 1, 4), (3, 2, 4),…….., (3, 6, 4), (4, 1, 4),
(4, 2, 4),……., (4, 6, 4), (5, 1, 4), (5, 2, 4),……(5, 6, 4),
(6, 1, 4), (6, 2, 4),……….(6, 6, 4)} .
B = {(6, 5, 1), (6, 5, 2), (6, 5, 3), (6, 5, 4), (6, 5, 5), (6, 5, 6)}
∴ A ∩ B = {(6, 5, 4)}

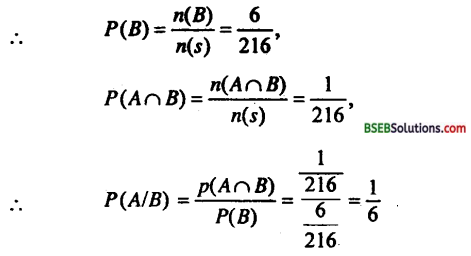
प्रश्न 20.
एक कलश में 10 काली तथा 5 उजली गेंदें हैं। दो गेंदें एक के बाद एक बिना कलश में डाले निकाले गये हैं तो प्रायिकता ज्ञात करें कि दोनों गेंदें काली है।
उत्तर:
माना कि E तथा F दो घटनाएं हैं जो प्रथम तथा दूसरे गेंद के काली होने की घटना है तो,
P(E ∩ F) = ?
∵ P(E) = \(\frac{n(E)}{n(s)}=\frac{10_{c_{1}}}{15_{c_{1}}}=\frac{10}{15}\)
अब एक गेंदे काली निकलने के बाद कलश में शेष 9 काली गेंदे होगें।
∴ \(p\left(\frac{F}{E}\right)=\frac{9_{c_{1}}}{14}=\frac{9}{14}\)
P(E ∩ E) = P(E).P(F/E)
= \(\frac{10}{15} \times \frac{9}{14}=\frac{3}{7}\)

प्रश्न 21.
एक पासे के दो उछाल में घटना A, प्रथम उछाल में विषम संख्या तथा घटना B द्वितीय उछाल में विषम संख्या आने की घटना है तो जाँचें कि घटनाA और B, स्वतंत्र घटनाएं हैं।
उत्तर:
एक पासे के दो उछाल में n(s) = 6 × 6 = 36
∵ एक पासे में तीन विषम संख्याएँ होती है।
∴ n(A) = 3 × 6 = 18, n (B) = 3 × 6 = 18
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{18}{36}=\frac{1}{2}\), P(B) = \(\frac{1}{2}\)

∴ P(A ∩ B) = P(A) × P(B)
∵ A और B परस्पर स्वतंत्र घटनाएं हैं।

प्रश्न 22.
तीन सिक्कों के उछाल में, तीन heads या तीन tails होने की घटना E हो, कम से कम दो heads होने की घटना F हो तथा अधिक से अधिक दो heads होने की घटना G हो तो (E, F), (E, G) तथा (F, G) में कौन जोड़ा स्वतंत्र घटना है और कौन जोड़ा स्वतंत्र घटना नहीं है।
उत्तर:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TIT}
E = {HHH, TIT}
F = {HHH, HHT, HTH, THH}
G = {HHT, HTH, THH, HTT, THT, TTH, TTT}
E ∩ F = {HHH}, E ∩ G = {TTT),
F ∩ G = {HHT, HTH, THH} .
∴ n (s) = 8, n (E) = 2, n (F) = 4, n (G) = 7, n (E ∩ F) = 1,
n (E ∩ G) = 1, n (F ∩ G) = 3

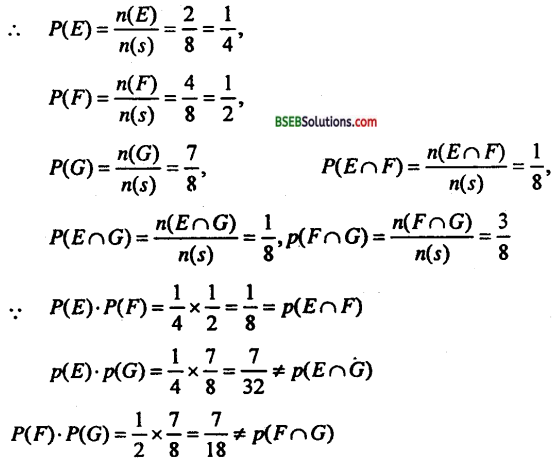
अतः घटना (E and F) स्वतंत्र घटना है तथा (E and G), (F and G) स्वतंत्र घटनाएँ नहीं है।

प्रश्न 23.
यदि E तथा F परस्पर स्वतंत्र घटनाएँ हो तो सिद्ध करें कि E तथा Flभी स्वतंत्र घटनाएँ हैं। .
उत्तर:
E तथा F स्वतंत्र घटनाएं हैं।
∴ P(E ∩ F) = P(E). P(F)

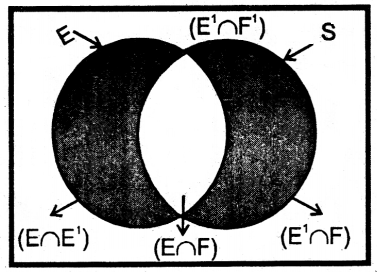
चित्र से, स्पष्ट है कि,
(E ∩ F) तथा (E ∩ F¹) परस्पर exclusive घटना है तथा
E = (E ∩ F) ∪(E ∩ F¹)
∴ P(E) = P(E ∩ F) + (P ∩ F¹)
या, P(E ∩ F¹) = p(E)- P(E ∩ F) = P(E) – P(E). P(F)
= p(E) ∙ (1 – p(F))
= p(E) ∙ p(F)
∴E तथा F¹ परस्पर स्वतंत्र घटनाएं हैं।

प्रश्न 24.
एक गड्डी में दो पत्ते बिना replacement के खींचे गये हैं तो बादशाह की संख्या – Mean variance तथा Standard deviation ज्ञात करें।
उत्तर:
माना कि x = No. of Kings in a draw of two cards.

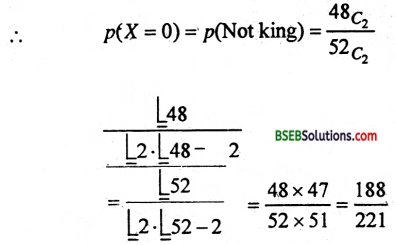
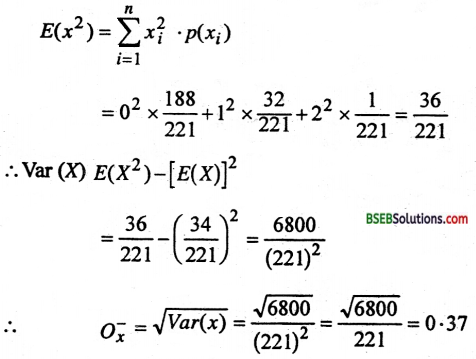
प्रश्न 25.
एक Lot जिसमें 10% टूटे अंडे हैं से बिना Replacement के 10 अंडे Successively निकाले गये हैं तो कम से कम एक टूटे अंडे निकलने का प्रायिकता ज्ञात करें।
उत्तर:
माना कि X = निकाले गये 10 अंडे में टूटे अंडे की संख्या
∴ n = 10, p = \(\frac{10}{100}\) = \(\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}=\frac{10-1}{10}=\frac{9}{10}\)
∴ P (at least one defective egg) = P(x ≥ 1)
= 1 – p (x = 0)

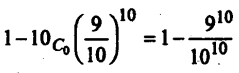
प्रश्न 26.
एक व्यक्ति एक निर्माण कम्पनी में नौकरी पर लगता है। उसके Strike होने की प्रायिकता 0.65 है ! यदि व्यक्ति Strike नहीं करता है तो Construction job के समय पर पूरा होने की प्रायिकता 0.80 है। यदि व्यक्ति Strike करता है तो काम के समय पर पूरा होने की प्रायिकता 0.32 है तो समय पर काम के पूरा होने की प्रायिकता ज्ञात करें।
उत्तर:
माना कि A = Construction Job के समय पर पूरा होने की घटना है।
B= व्यक्ति के Strike करने की घटना है तो P (A) = ?
दिया गया है-p (B) = 0.65, P (no Strike) = p(B¹)
= 1 – p(B)
= 1 – 0.65 = 0:35
P(A/B) = 0.32, p(A/B¹) = 0.80
∵ B तथा Bl Partition Form है।
∴ Total Probability Theorem से।
P(A) = p(B) ∙ p(A/B) + p(B¹) ∙ P(A/B¹)
= 0.65 × 0.32 + 0.35 × 0.8
= 0.208 + 0.28 = 0.488