Bihar Board Class 10 Maths Solutions Chapter 2 बहुपद Additional Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 2 बहुपद Additional Questions
Bihar Board Class 10 Maths बहुपद Additional Questions
बहुविकल्पीय प्रश्न
प्रश्न 1.
यदि द्विघात बहुपद (k – 1)x2 + kx + 1 के शून्यकों में से एक शून्यक -3 है, तो k का मान है
(i) \(\frac{4}{3}\)
(ii) \(\frac{-4}{3}\)
(iii) \(\frac{2}{3}\)
(iv) \(\frac{-2}{3}\)
हल
(i) \(\frac{4}{3}\)
प्रश्न 2.
शून्यक -3 और 4 वाला द्विघात बहुपद है
(i) x2 – x + 12
(ii) x2 + x + 12
(iii) \(\frac{x^{2}}{2}-\frac{x}{2}-6\)
(iv) 2x2 + 2x – 24
हल
(iii) \(\frac{x^{2}}{2}-\frac{x}{2}-6\)
![]()
प्रश्न 3.
यदि द्विघात बहुपद x2 + (a + 1)x + b के शून्यक 2 और -3 हैं, तो
(i) a = -7, b = -1
(ii) a = 5, b = -1
(iii) a = 2, b = -6
(iv) a = 0, b = -6
हल
(iv) a = 0, b = -6
प्रश्न 4.
शून्यक -2 और 5 वाले बहुपदों की संख्या है
(i) 1
(ii) 2
(iii) 3
(iv) 3 से अधिक
हल
(iv) 3 से अधिक
![]()
प्रश्न 5.
त्रिघात बहुपद ax3 + bx2 + cx + d का एक शून्यक 0 दिया हुआ है। अन्य दोनों शून्यकों का गुणनफल है
(i) \(-\frac{c}{a}\)
(ii) \(\frac{c}{a}\)
(iii) 0
(iv) \(-\frac{b}{a}\)
हल
(ii) \(\frac{c}{a}\)
प्रश्न 6.
यदि त्रिघात बहुपद x3 + ax2 + bx + c का एक शून्यक -1 है, तो अन्य दोनों शून्यकों का गुणनफल है
(i) b – a + 1
(ii) b – a – 1
(iii) a – b + 1
(iv) a – b – 1
हल
(i) b – a + 1
प्रश्न 7.
द्विघात बहुपद x2 + 99x + 127 के शून्यक हैं
(i) दोनों धनात्मक
(ii) दोनों ऋणात्मक
(iii) एक धनात्मक और एक ऋणात्मक
(iv) दोनों बराबर
हल
(ii) दोनों ऋणात्मक
![]()
प्रश्न 8.
द्विघात बहपद x2 + kx + k, k ≠ 0 के शून्यक
(i) दोनों धनात्मक नहीं हो सकते
(ii) दोनों ऋणात्मक नहीं हो सकते
(iii) सदैव असमान होते हैं
(iv) सदैव बराबर होते हैं
हल
(i) दोनों धनात्मक नहीं हो सकते
प्रश्न 9.
यदि द्विघात बहुपद ax2 + bx + c, c ≠ 0 के शून्यक बराबर हैं, तो
(i) c और a विपरीत चिह्नों के हैं
(ii) c और b विपरीत चिह्नों के हैं
(iii) c और a एक ही चिह्न के हैं
(iv) c और b एक ही चिह्न के हैं
हल
(iii) c और a एक ही चिह्न के हैं
प्रश्न 10.
यदि x2 + ax + b के रूप के एक द्विघात बहुपद का एक शून्यक दूसरे शून्यक का ऋणात्मक हो, तो
(i) इसमें कोई रैखिक पद नहीं होता तथा अचर पद ऋणात्मक होता है।
(ii) इसमें कोई रैखिक पद नहीं होता तथा अचर पद धनात्मक होता है।
(iii) इसका रैखिक पद हो सकता है, परन्तु अचर पद ऋणात्मक होता है
(iv) इसका रैखिक पद हो सकता है, परन्तु अचर पद धनात्मक होता है
हल
(i) इसमें कोई रैखिक पद नहीं होता तथा अचर पद ऋणात्मक होता है।
![]()
प्रश्न 11.
निम्नलिखित में से कौन एक द्विघात बहुपद का आलेख नहीं है?
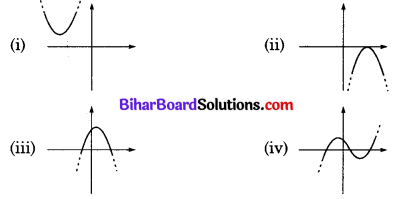
हल
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
यदि -2 बहुपद 9x3 + 18x2 – x – 2 का एक शून्यक हो तो इस बहुपद के सभी शून्यक ज्ञात कीजिए।
हल
यदि -2 बहुपद 9x3 + 18x2 – x – 2 का एक शून्यक हो तो x + 2 बहुपद 9x3 + 18x2 – x – 2 का एक गुणनखण्ड होगा।
तब, 9x3 + 18x2 – x – 2
= 9x2 (x + 2) – 1(x + 2)
= (x + 2) (9x2 – 1)
= (x + 2) (3x + 1) (3x -1)
3x + 1 और 3x – 1 को शून्य के बराबर करने पर,
x = \(-\frac{1}{3}\) तथा x = \(\frac{1}{3}\)
अतः दिए गए बहुपद 9x3 + 18x2 – x – 2 के शून्यक = -2, \(\frac{1}{3}\) व \(-\frac{1}{3}\) हैं।
![]()
प्रश्न 2.
जाँच कीजिए कि बहुपद के साथ दी गई संख्या उसकी शून्यक है अथवा नहीं?
x2 – 2√3x – 9, x = 3√3, x = -√3
हल
दिया गया बहुपद
= x2 – 2√3x – 9
= x2 – (3√3 – √3)x – 9
= x2 – 3√3x + √3x – (3√3 × √3)
= x(x – 3√3) + √3(x – 3√3)
= (x – 3√3) (x + √3)
उक्त बहुपद शून्य तब होगा जब x – 3√3 = 0 अर्थात् x = 3√3 हो
या फिर उक्त बहुपद शून्य तब होगा जब x + √3 = 0 हो अर्थात् x = -√3 हो।
अत: संख्याएँ x = 3√3 व x = -√3 दिए बहुपद x2 – 2√3x – 9 की शून्यक हैं।
प्रश्न 3.
बहुपद x3 + 2x2 – x – 2 का एक शून्यक (-2) है तो सभी शून्यक ज्ञात कीजिए।
हल
बहुपद x3 + 2x2 – x – 2 का एक शून्यक (-2) है
(x + 2) बहुपद का एक गुणनखण्ड है।
x3 + 2x2 – x – 2 = x2(x + 2) – 1(x + 2)
= (x + 2)(x2 – 1)
= (x + 2)(x + 1) (x – 1)
बहुपद x3 + 2x2 – x – 2 के शून्य होने के लिए
x + 1 = 0 ⇒ x = -1
x – 1 = 0 ⇒ x = 0
अत: बहुपद x3 + 2x2 – x – 2 के शून्यक = -2, -1 व 1 हैं।
![]()
प्रश्न 4.
बहुपद x2 – 9 के शून्यक ज्ञात कीजिए।
हल
बहुपद x2 – 9 के गुणनखण्ड करने पर,
x2 – 9 = (x)2 – (3)2 = (x + 3) (x – 3)
x2 – 9 के शून्य होने के लिए।
x + 3 = 0 ⇒ x = -3
तथा x – 3 = 0 ⇒ x = 3
अत: x2 – 9 के शून्यक = -3 व 3
प्रश्न 5.
चित्र में, बहुपद y = f(x) का आलेख दिया गया है। इसके शून्यकों की संख्या बताइए।
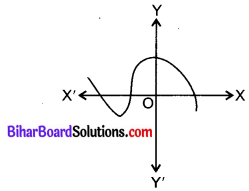
हल
बहुपद y = f(x) का आलेख X-अक्ष को 3 बिन्दुओं पर काटता है। अत: शून्यकों की संख्या 3 है।
प्रश्न 6.
यदि बहुपद ax2 – 6x – 6 के शून्यकों का गुणनफल 6 हो तो a का मान ज्ञात कीजिए।
हल
दिया गया बहुपद = ax2 – 6x – 6
तथा शून्यकों का गुणनफल = 6

![]()
प्रश्न 7.
बहुपद x3 – 3x2 + 5x – 3 को x – 1 से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए।
हल
बहुपद x3 – 3x2 + 5x – 3 = p(x), भाजक = x – 1 = g(x)
माना भागफल q(x) तथा शेषफल r(x) है।
अब, बहुपद को भाजक से भाग देने पर,
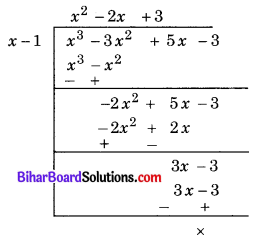
अत: भागफल q(x) = x2 – 2x + 3 तथा शेषफल r(x) = शून्य।
लघु उत्तरीय प्रश्न
प्रश्न 1.
एक द्विघात बहुपद ज्ञात कीजिए जिसके शून्यकों का योगफल तथा गुणनफल क्रमशः 0 तथा √5 हैं।
हल
माना द्विघात बहुपद ax2 + bx + c है और इसके शून्यक α व β हैं।
तब, α + β = \(-\frac{b}{a}\) और αβ = \(\frac{c}{a}\)
प्रश्नानुसार, शून्यकों का योगफल (α + β) = \(-\frac{b}{a}\)
तथा शून्यकों का गुणनफल (αβ) = \(\frac{c}{a}\) = √5
यदि a = 1 हो तो b = 0, तथा c = √5
अत: एक मानक द्विघात बहुपद ax2 + bx + c में
a = 1, b = 0 तथा c = √5
प्रतिस्थापित करने पर,
बहुपद = x2 + 0 . x + √5 = x2 + √5
अत: अभीष्ट बहुपद = x2 + √5
उक्त प्रतिबन्धों को सन्तुष्ट करने वाला व्यापक द्विघात व्यंजक = k(x2 + √5), जहाँ k एक वास्तविक संख्या है।
![]()
प्रश्न 2.
एक द्विघात बहुपद ज्ञात कीजिए जिसके शून्यकों के योगफल तथा गुणनफल क्रमशः संख्याएँ -1, 1 हैं।
हल
माना द्विघात बहुपद के शून्यक α तथा β हैं।
तब, शून्यकों का योगफल = α + β
तथा शून्यकों का गुणनफल = αβ
प्रश्नानुसार, शून्यकों का योगफल (α + β) = -1
शून्यकों का गुणनफल (αβ) = +1
द्विघात बहुपद = (x – α) (x – β)
= x2 – (α + β) x + αβ
= x2 – (-1) . x + (+1)
= x2 + x + 1
अतः अभीष्ट बहुपद = x2 + x + 1
प्रश्न 3.
द्विघात बहुपद 6x2 – 7x – 3 के शून्यक ज्ञात कीजिए।
हल
दिया गया द्विघात बहुपद = 6x2 – 7x – 3
गुणनखण्ड करने पर,
6x2 – 7x – 3
= 6x2 – 9x + 2x – 3
= 3x(2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
इसलिए 6x2 – 7x – 3 शून्य होगा यदि
2x – 3 = 0 अथवा 3x + 1 = 0
अर्थात् 2x – 3 = 0 ⇒ x = \(\frac{3}{2}\)
अथवा 3x + 1 = 0 ⇒ x = \(-\frac{1}{3}\)
अत: बहुपद 6x2 – 7x – 3 के शून्यक \(\frac{3}{2}\) व \(-\frac{1}{3}\) हैं।
![]()
प्रश्न 4.
द्विघात बहुपद 2x2 – 50 के शून्यक ज्ञात कीजिए।
हल
बहुपद 2x2 – 50 के गुणनखण्ड करने पर,
2x2 – 50 = 2(x2 – 25)
= 2[(x)2 – (5)2]
= 2(x + 5) (x – 5)
2x2 – 50 के शून्य होने के लिए
x + 5 = 0 ⇒ x = -5
तथा x – 5 = 0 ⇒ x = 5
अत: 2x2 – 50 के शून्यक -5 व 5 हैं।
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
2x4 – 3x3 – 3x2 + 6x – 2 के अन्य सभी शून्यक ज्ञात कीजिए यदि इसके दो शून्यक √2 और -√2 ज्ञात हैं।
हल
बहुपद 2x4 – 3x3 – 3x2 + 6x – 2 के दो शून्यक √2 व -√2 हैं और माना दो अन्य शून्यक α व β हैं।
(x – α) (x – β) (x – √2) (x – (-√2)) = 2x4 – 3x3 – 3x2 + 6x – 2
(x – α) (x – β) (x – √2) (x + √2) = 2x4 – 3x3 – 3x2 + 6x – 2
(x – α) (x – β) (x2 – 2) = 2x4 – 3x3 – 3x2 + 6x – 2

![]()
प्रश्न 2.
द्विघात बहुपद 6x2 – 13x + 6 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए।
हल
दिया गया द्विघात बहुपद = 6x2 – 13x + 6
गुणनखण्ड करने पर,
6x2 – 13x + 6 = 6x2 – (9 + 4)x + 6
= 6x2 – 9x – 4x + 6
= 3x(2x – 3) – 2(2x – 3)
= (2x – 3) (3x – 2)
इसलिए 6x2 – 13x + 6 शून्य होगा, यदि 2x – 3 = 0 है तथा 3x – 2 = 0 है।
अर्थात् 2x – 3 = 0 ⇒ x = \(\frac{3}{2}\)
तथा 3x – 2 = 0 ⇒ x = \(\frac{2}{3}\)
बहुपद 6×2 – 13x + 6 के शून्यक \(\frac{3}{2}\) तथा \(\frac{2}{3}\) हैं।

तब, समीकरण (1) व (3) से,
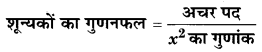
तथा समीकरण (2) व (4) से,

अत: बहुपद के शून्यकों और गुणांकों के बीच के उपर्युक्त सम्बन्ध सत्य हैं।