Bihar Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Additional Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Additional Questions
Bihar Board Class 10 Maths दो चरों वाले रैखिक समीकरण युग्म Additional Questions
बहुविकल्पीय प्रश्न
प्रश्न 1.
आलेखीय रूप से,
6x – 3y + 10 = 0
2x – y + 9 = 0
समीकरणों का युग्म दो रेखाएँ निरूपित करता है, जो
(i) ठीक एक बिन्दु पर प्रतिच्छेद करती हैं
(ii) ठीक दो बिन्दुओं पर प्रतिच्छेद करती हैं
(iii) संपाती हैं
(iv) समांतर हैं
हल
(iv) समांतर हैं
प्रश्न 2.
समीकरण x + 2y + 5 = 0 और -3x – 6y + 1 = 0 के युग्म
(i) का एक अद्वितीय हल है
(ii) के ठीक दो हल हैं
(iii) के अपरिमित रूप से अनेक हल हैं
(iv) का कोई हल नहीं है
हल
(iv) का कोई हल नहीं है
![]()
प्रश्न 3.
यदि रैखिक समीकरणों का कोई युग्म संगत है, तो इसके आलेख की रेखाएँ होंगी
(i) समान्तर
(ii) सदैव संपाती
(iii) प्रतिच्छेदी या संपाती
(iv) सदैव प्रतिच्छेदी
हल
(iii) प्रतिच्छेदी या संपाती
प्रश्न 4.
समीकरण y = 0 और y = -7 के युग्म
(i) का एक हल है
(ii) के दो हल हैं
(iii) अपरिमित रूप से अनेक हल हैं
(iv) का कोई हल नहीं है
हल
(iv) का कोई हल नहीं है
प्रश्न 5.
समीकरण x = a और y = b का युग्म आलेखीय रूप वे रेखाएँ निरूपित करता है, जो
(i) समांतर हैं
(ii) (b, a) पर प्रतिच्छेद करती हैं
(iii) संपाती हैं
(iv) (a, b) पर प्रतिच्छेद करती हैं
हल
(iv) (a, b) पर प्रतिच्छेद करती हैं
![]()
प्रश्न 6.
k के किस मान के लिए समीकरण 3x – y + 8 = 0 और 6x – ky = -16 संपाती रेखाएँ निरूपित करते हैं?
(i) \(\frac{1}{2}\)
(ii) \(\frac{-1}{2}\)
(iii) 2
(iv) -2
हल
(iii) 2
प्रश्न 7.
यदि 3x + 2ky = 2 और 2x + 5y + 1 = 0 द्वारा दी जाने वाली रेखाएँ परस्पर समांतर हैं, तो k का मान है
(i) \(\frac{-5}{4}\)
(ii) \(\frac{2}{5}\)
(iii) \(\frac{15}{4}\)
(iv) \(\frac{3}{2}\)
हल
(ii) \(\frac{2}{5}\)
प्रश्न 8.
c का वह मान, जिसके लिए समीकरणों cx – y = 2 और 6x – 2y = 3 के युग्म के अपरिमित रूप से अनेक हल होंगे, है
(i) 3
(ii) -3
(iii) -12
(iv) कोई मान नहीं
हल
(iv) कोई मान नहीं
![]()
प्रश्न 9.
आश्रित रैखिक समीकरणों के युग्म का एक समीकरण -5x + 7y = 2 है। दूसरा समीकरण हो सकता है
(i) 10x + 14y + 4 = 0
(ii) -10x – 14y + 4 = 0
(iii) -10x + 14y + 4 = 0
(iv) 10x – 14y = -4
हल
(iv) 10x – 14y = -4
प्रश्न 10.
एक अद्वितीय हल x = 2, y = -3 वाले समीकरण का एक युग्म है
(i) x + y = -1
2x – 3y = -5
(ii) 2x + 5y = -11
4x + 10y = -22
(iii) 2x – y = 1
3x + 2y = 0
(iv) x – 4y – 14 = 0
5x – y – 13 = 0
हल
(ii) 2x + 5y = -11
4x + 10y = -22
प्रश्न 11.
यदि x = a और y = b समीकरणों x – y = 2 और x + y = 4 का हल है, तो a और b के मान क्रमशः हैं
(i) 3 और 5
(ii) 5 और 3
(iii) 3 और 1
(iv) -1 और -3
हल
(iii) 3 और 1
![]()
प्रश्न 12.
अरुणा के पास केवल 1 और ₹ 2 के सिक्के हैं। यदि उसके पास कुल 50 सिक्के हैं तथा कुल धनराशि ₹ 75 है, तो ₹ 1 और ₹ 2 के सिक्कों की संख्याएँ क्रमशः हैं
(i) 35 और 15
(ii) 35 और 20
(iii) 15 और 35
(iv) 25 और 25
हल
(iv) 25 और 25
प्रश्न 13.
पिता की आयु पुत्र की आयु की 6 गुनी है। चार वर्ष के बाद, पिता की आयु अपने पुत्र की आयु की चार गुनी होगी। पुत्र और पिता की वर्तमान आयु (वर्षों में ) क्रमशः हैं
(i) 4 और 24
(ii) 5 और 30
(iii) 6 और 36
(iv) 3 और 24
हल
(iii) 6 और 36
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
दिखाइए कि निम्न रैखिक समीकरण युग्म का एक अद्वितीय हल है।
3x – 4y = 10 तथा 4x + 3y = 5
हल
दिए गए रैखिक समीकरणों का युग्म
3x – 4y – 10 = 0 …….. (1)
4x + 3y – 5 = 0 …….(2)
उपर्युक्त समीकरण युग्म की तुलना रैखिक समीकरण युग्म a1x + b1y + c1y = 0 तथा a2x + b2y + c2 = 0 से करने पर,

दिए गए समीकरण युग्म का एक अद्वितीय हल है।
![]()
प्रश्न 2.
बिना ग्राफ की सहायता के बताइए कि रेखाएँ 4x + 6y – 18 = 0 और 2x + 3y – 6 = 0 प्रतिच्छेदी हैं या सम्पाती हैं या समान्तर हैं?
हल
दिए गए समीकरणों का युग्म
4x + 6y – 18 = 0 ……(1)
2x + 3y – 6 = 0 …….(2)
उपर्युक्त समीकरण युग्म की तुलना रैखिक समीकरण युग्म a1x + b1y + c1 = 0 तथा a2x + b2y + c2 = 0 से करने पर,

अत: समीकरण युग्म द्वारा निरूपित ऋजु रेखाएँ समान्तर हैं।
प्रश्न 3.
किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए ₹ 700 की राशि रखी गई है। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹ 20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
हल
माना सबसे कम पुरस्कार की राशि ₹ x हैं।
7 पुरस्कारों का मूल्य = ₹ x , ₹ (x + 20), ₹ (x + 40), ₹ (x + 60), ₹ (x + 80) , ₹ (x + 100), ₹ (x + 120)
प्रश्नानुसार, x + x + 20 + x + 40 + x + 60 + x + 80 + x + 100 + x + 120 = 700
⇒ 7x + 420 = 700
⇒ 7x = 700 – 420 = 280
⇒ x = 40
अतः पुरस्कारों की राशि ₹ 40, ₹ 60 , ₹ 80 , ₹ 100 ,₹ 120 , ₹ 140 तथा ₹ 160 है।
लघु उत्तरीय प्रश्न
प्रश्न 1.
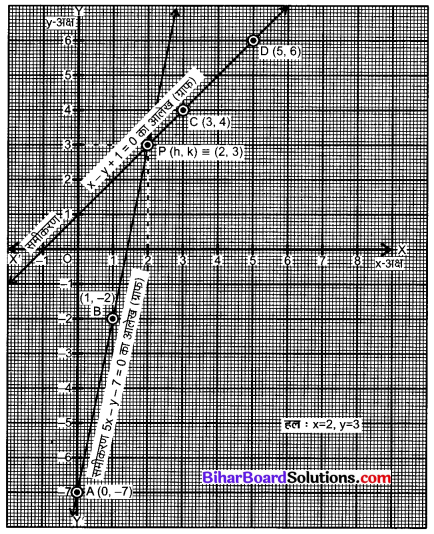
निम्नलिखित समीकरण युग्म को ग्राफीय विधि से हल कीजिए-
5x – y – 7 = 0 तथा x – y + 1 = 0
हल
1. दिए हुए समीकरण युग्म का पहला समीकरण
5x – y – 7 = 0
2. माना x = 0, तब x का यह मान समीकरण 5x – y – 7 = 0 में रखने पर,
(5 × 0) – y – 7 = 0
⇒ 0 – y – 7 = 0
⇒ y = -7
3. तब समीकरण 5x – y – 7 = 0 के आलेख पर एक बिन्दु A = (0, -7)
4. पुनः माना x = 1, तब x का यह मान समीकरण 5x – y – 7 = 0 में रखने पर,
(5 × 1) – y – 7 = 0
⇒ 5 – y – 7 = 0
⇒ y = -2
5. तब समीकरण 5x – y – 7 = 0 के आलेख पर एक बिन्दु B = (1, -2)
6. ग्राफ पेपर पर बिन्दुओं A = (0, -7) तथा B = (1, -2) का आलेखन (plotting) कीजिए और दिए हुए समीकरण का आलेख ऋजु रेखा AB खींचिए।
7. दिए हुए समीकरण युग्म का दूसरा समीकरण x – y + 1 = 0
8. माना x = 3, तब x का यह मान समीकरण x – y + 1 = 0 में रखने पर,
3 – y + 1 = 0
⇒ 3 + 1 = 0 + y
⇒ y = 4
9. तब समीकरण x – y + 1 = 0 के आलेख पर एक बिन्दु C = (3, 4)
10. पुन: माना x = 5, तब x का यह मान समीकरण x – y + 1 = 0 में रखने पर,
5 – y + 1 = 0 या 5 + 1 = 0 + y या y = 6
11. तब समीकरण x – y + 1 = 0 के आलेख पर एक बिन्दु D = (5, 6)
12. उन्हीं निर्देशाक्षों, जिन पर समीकरण 5x – y – 7 = 0 का आलेख खींचा है, पर बिन्दुओं C = (3, 4) व D = (5, 6) का आलेखन कीजिए और समीकरण x – y + 1 = 0 का आलेख ऋजु रेखा CD खींचिए।
13. ऋजु रेखाओं AB और CD के प्रतिच्छेद बिन्दु P(h, k) के निर्देशांक आलेख की सहायता से पढ़िए। यहाँ P(h, k) = (2, 3)
अत: दिए गए समीकरण युग्म का हल x = 2, y = 3
![]()
प्रश्न 2.
समीकरण युग्म x + 3y = 6 और 2x – 3y = 12 के लिए दिए गए आलेखन को देखिए और अपनी उत्तर-पुस्तिका में निम्न प्रश्नों के उत्तर लिखिए-
(a) समीकरण युग्मों का हल क्या है?
(b) समीकरण युग्मों और Y-अक्ष से निर्मित क्षेत्र का क्षेत्रफल कितना है?
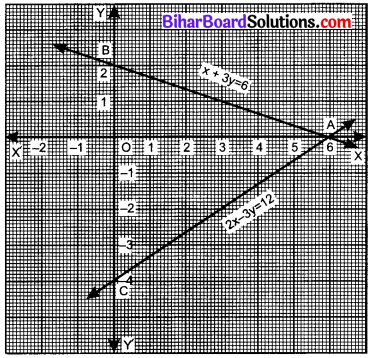
हल
(a) ग्राफ से स्पष्ट है कि समीकरण युग्मों का प्रतिच्छेद बिन्दु (6, 0) है,
अत: समीकरण युग्मों का हल x = 6 तथा y = 0
(b) त्रिभुज के शीर्ष A(6, 0), B(0, 2) तथा C(0, -4) हैं।
अतः त्रिभुज के आधार की लम्बाई BC = OC + OB = 4 + 2 = 6
त्रिभुज की ऊँचाई OA = 6
अत: त्रिभुज का क्षेत्रफल = Δ = \(\frac {1}{2}\) × BC × OA
= \(\frac {1}{2}\) × 6 × 6
= 18 वर्ग मात्रक
प्रश्न 3.
समीकरणों √x + √y = 5 तथा x + y = 13 को हल कीजिए।
हल
दिए गए समीकरणों का युग्म
√x + √y = 5 ……..(1)
x + y = 13 …….. (2)
समीकरण (2) से,
y = 13 – x ……..(3)
समीकरण (1) में y का मान रखने पर,
√x + \(\sqrt{13-x}\) = 5
दोनों पक्षों का वर्ग करने पर,

पुन: दोनों पक्षों का वर्ग करने पर,
13x – x2 = 36
⇒ x2 – 13x + 36 = 0
⇒ x2 – (4x + 9x) + 36 = 0
⇒ x2 – 4x – 9x + 36 = 0
⇒ x(x – 4) – 9(x – 4) = 0
⇒ (x – 4) (x – 9) = 0
द्विपद x2 – 13x + 36 को शून्य होने के लिए,
x – 4 = 0 = x = 4
x – 9 = 0 = x = 9
समीकरण (3) में x = 4 रखने पर, y = 13 – 4 = 9
पुन: समीकरण (3) में x = 9 रखने पर, y = 13 – 9 = 4
अतः समीकरण युग्म का हल
x = 4, 9 तथा y = 9, 4
![]()
प्रश्न 4.
समीकरणों \(\frac{1}{x}+\frac{2}{y}=3\) और \(\frac{2}{x}-\frac{4}{y}=2\) को हल कीजिए।
हल
दिए गए समीकरणों का युग्म

समीकरण (1) तथा समीकरण (2) को जोड़ने पर,
![]()
समीकरण (1) में से समीकरण (2) को घटाने पर,
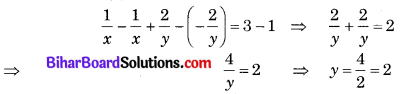
अत: समीकरणों के युग्म का हल x = \(\frac{1}{2}\) तथा y = 2
प्रश्न 5.
6 वर्ष बाद एक आदमी की आयु उसके पुत्र की आयु की 3 गुनी हो जाएगी और 3 वर्ष पूर्व वह अपने पुत्र की आयु का 9 गुना था। उनकी वर्तमान आयुज्ञात कीजिए।
हल
माना आदमी की वर्तमान आयु x वर्ष है और उसके पुत्र की वर्तमान आयु y वर्ष है।
तब, 6 वर्ष के बाद उस आदमी की आयु = (x + 6) वर्ष
तथा 6 वर्ष के बाद उस आदमी के पुत्र की आयु = (y + 6) वर्ष
प्रश्नानुसार, 6 वर्ष बाद आदमी की आयु = 3 × (6 वर्ष बाद उस आदमी के पुत्र की आयु)
(x + 6) = 3(y + 6)
⇒ x + 6 = 3y + 18
⇒ x – 3y = 12 …….(1)
3 वर्ष पूर्व उस आदमी की आयु = (x – 3) वर्ष
और 3 वर्ष पूर्व उस आदमी के पुत्र की आयु = (y – 3) वर्ष
तब प्रश्नानुसार, 3 वर्ष पूर्व उस आदमी की आयु = 9 × (3 वर्ष पूर्व उस आदमी के पुत्र की आयु)
(x – 3) = 9 × (1 – 3)
⇒ x – 3 = 9y – 27
⇒ x = 9y – 27 + 3
⇒ x = 9y – 24 ……(2)
समीकरण (2) से x का मान समीकरण (1) में रखने पर,
9y – 24 – 3y = 12
⇒ 6y = 12 + 24
⇒ 6y = 36
⇒ y = 6
समीकरण (2) में y का मान रखने पर,
x = (9 × 6) – 24 = 54 – 24 = 30
अतः आदमी की वर्तमान आयु = 30 वर्ष
तथा उसके पुत्र की वर्तमान आयु = 6 वर्ष।
![]()
प्रश्न 6.
एक आयताकार खेत का परिमाप 50 मीटर एवं क्षेत्रफल 100 वर्ग मीटर है। खेत की लम्बाई एवं चौड़ाई ज्ञात कीजिए।
हल
माना खेत की लम्बाई x मीटर तथा चौड़ाई y मीटर है।
खेत का परिमाप = (2x + 2y) मीटर = 2(x + y) मीटर
प्रश्नानुसार,
2(x + y) = 50
⇒ x + y = 25
⇒ y = 25 – x
खेत का क्षेत्रफल = xy वर्ग मीटर
प्रश्नानुसार, xy = 100 ……(2)
समीकरण (1) से y का मान समीकरण (2) में रखने पर,
x(25 – x) = 100
⇒ 25x – x2 – 100 = 0
⇒ x2 – 25x + 100 = 0
⇒ x2 – (20x + 5x) + 100 = 0
⇒ x2 – 20x – 5x + 100 = 0
⇒ x(x – 20) – 5(x – 20) = 0
⇒ (x – 20) (x – 5) = 0
समीकरण x2 – 25x + 100 के शून्य होने के लिए,
x – 20 = 0 ⇒ x = 20
x – 5 = 0 ⇒ x = 5
समीकरण (1) में x = 20 रखने पर, y = 25 – 20 = 5
खेत की लम्बाई = 20 मीटर तथा चौड़ाई = 5 मीटर।
प्रश्न 7.
एक मोटरबोट, जिसकी स्थिर जल में चाल 18 km/h है, 24 km धारा के प्रतिकूल जाने में, वही दूरी धारा के अनुकूल जाने की अपेक्षा 1 घण्टा अधिक लेती है। धारा की चाल ज्ञात कीजिए।
हल
माना धारा की चाल = x km/h
धारा के प्रतिकूल मोटरबोट की चाल = (18 – x) km/h
तथा धारा के अनुकूल मोटरबोट की चाल = (18 + x) km/h
धारा के प्रतिकूल जाने में लगा समय = \(\frac{\text { दूरी }}{\text { चाल }}\) = \(\frac{24}{18-x}\) घंटे
इसी प्रकार, धारा के अनुकूल जाने में लगा समय = \(\frac{24}{18+x}\) घंटे
प्रश्नानुसार, \(\frac{24}{18-x}-\frac{24}{18+x}=1\)
⇒ \(\frac{24(18+x)-24(18-x)}{(18-x)(18+x)}=1\)
⇒ 24(18 + x – 18 + x) = 324 – x2
⇒ 24 × (2x) + x2 – 324 = 0
⇒ x2 + 48x – 324 = 0
⇒ x2 + (54x – 6x) – 324 = 0
⇒ x2 + 54x – 6(x + 54) = 0
⇒ x(x + 54) – 6(x + 54) = 0
⇒ (x – 6) (x + 54) = 0
अब x2 + 48x – 324 के शून्य होने के लिए
x – 6 = 0 ⇒ x = 6
x + 54 = 0 ⇒ x = -54 असम्भव
धारा की चाल = 6 km/h
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
एक नाव 10 घंटे में धारा के प्रतिकूल 30 km तथा धारा के अनुकूल 44 km जाती है। 13 घंटे में वह 40 km धारा के प्रतिकूल एवं 55 km धारा के अनुकूल जाती है। धारा की चाल तथा नाव की स्थिर पानी में चाल ज्ञात कीजिए।
हल
माना नाव की स्थिर पानी में चाल x km/h और धारा की चाल y km/h है।
तब, धारा के अनुकूल नाव चलाने की चाल = (x + y) km/h
और धारा के प्रतिकूल नाव चलाने की चाल = (x – y) km/h
धारा के प्रतिकूल 30 km दूरी चलने में लगा समय = \(\frac{30}{x-y}\) घंटे
और धारा के अनुकूल 44 km दूरी चलने में लगा समय = \(\frac{44}{x+y}\) घंटे
प्रश्नानुसार, दोनों समयों का योग = 10 घंटे

इसी प्रकार, धारा के प्रतिकूल 40 km दूरी चलने में लगा समय = \(\frac{40}{x-y}\) घंटे
तथा धारा के अनुकूल 55 km दूरी चलने में लगा समय = \(\frac{55}{x+y}\) घंटे
प्रश्नानुसार, दोनों समयों का योग = 13 घंटे

समीकरण (4) में समीकरण (5) को जोड़ने पर, 2x = 16 ⇒ x = 8
समीकरण (5) में से समीकरण (4) को घटाने पर, 2y = 6 ⇒ y = 3
अत: धारा की चाल 3 km/h तथा नाव की स्थिर पानी में चाल 8 km/h है।
![]()
प्रश्न 2.
बंगलुरू के एक बस स्टैण्ड से यदि हम 2 टिकट मल्लेश्वरम के तथा 3 टिकट यशवंतपुर के खरीदें तो कुल लागत ₹ 46 है। परन्तु यदि हम 3 टिकट मल्लेश्वरम् के और 5 टिकट यशवंतपुर के खरीदें तो कुल लागत ₹ 74 है। बस स्टैण्ड से मल्लेश्वरम का किराया तथा बस स्टैण्ड से यशवंतपुर का किराया ज्ञात कीजिए।
हल
माना बस स्टैण्ड से मल्लेश्वरम् का किराया ₹ x तथा बस स्टैण्ड से यशवंतपुर का किराया ₹ y है।
बस स्टैण्ड से मल्लेश्वरम् का किराया ₹ x है।
मल्लेश्वरम् के 2 टिकटों का मूल्य = ₹ 2x
बस स्टैण्ड से यशवंतपुर का किराया = ₹ y
यशवंतपुर के 3 टिकटों का मूल्य = ₹ 3y
मल्लेश्वरम् के 2 टिकटों और यशवंतपुर के 3 टिकटों का मूल्य = ₹(2x + 3y)
परन्तु प्रश्नानुसार, इनका मूल्य ₹ 46 है।
2x + 3y = 46 ……(1)
बस स्टैण्ड से मल्लेश्वरम् का किराया ₹ x है।
मल्लेश्वरम् के 3 टिकटों का मूल्य = ₹ 3x
बस स्टैण्ड से यशवंतपुर का किराया ₹ y है।
यशवंतपुर के 5 टिकटों का मूल्य = ₹ 5y
मल्लेश्वरम् के 3 टिकटों और यशवंतपुर के 5 टिकटों का मूल्य = ₹ (3x + 5y)
परन्तु प्रश्नानुसार, उनका मूल्य ₹ 74 है।
3x + 5y = 74 ……… (2)
समीकरण (2) से,
3x + 5y = 74
⇒ 5y = 74 – 3x
⇒ y = \(\frac{74-3 x}{5}\) ……(2)
y का यह मान समीकरण (1) में रखने पर,

अत: बस स्टैण्ड से मल्लेश्वरम् का किराया ₹ 8 तथा बस स्टैण्ड से यशवंतपुर का किराया ₹ 10 है।