Bihar Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Additional Questions

Bihar Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Additional Questions and Answers.

BSEB Bihar Board Class 10 Maths Solutions Chapter 4 द्विघात समीकरण Additional Questions

Bihar Board Class 10 Maths द्विघात समीकरण Additional Questions

बहुविकल्पीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन-सा द्विघात समीकरण है?
(i) x² + 2x + 1 = (4 – x)² + 3
(ii) -2x² = (5 – x) (2x – \(\frac{2}{5}\))
(iii) (k + 1)x² + \(\frac{3}{2}\)x = 7, जहाँ, k = -1
(iv) x³ – x² = (x – 1)³
हल
(iv) x³ – x² = (x – 1)³

प्रश्न 2.
निम्नलिखित में से किस समीकरण का एक मूल 2 है?
(i) x² – 4x + 5 = 0
(ii) x² + 3x – 12 = 0
(iii) 2x² – 7x + 6 = 0
(iv) 3x² – 6x – 2 = 0
हल
(iii) 2x² – 7x + 6 = 0

प्रश्न 3.
यदि समीकरण x² + kx – \(\frac{5}{4}\) = 0 का एक मूल \(\frac{1}{2}\) है, तो k का मान है
(i) 2
(ii) -2
(iii) \(\frac{1}{4}\)
(iv) \(\frac{1}{2}\)
हल
(i) 2

प्रश्न 4.
k के वे मान, जिनके लिए द्विघात समीकरण 2x² – kx + k = 0 के मूल बराबर होंगे, निम्नलिखित हैं
(i) केवल 0
(ii) 4
(iii) केवल 8
(iv) 0, 8
हल
(iv) 0, 8

प्रश्न 5.
पूर्ण वर्ग बनाने की विधि द्वारा द्विघात समीकरण 9x² + \(\frac{3}{4}\)x – √2 = 0 को हल करने के लिए, इसमें किस अचर को जोड़ना और घटाना चाहिए?
(i) \(\frac{1}{8}\)
(ii) \(\frac{1}{64}\)
(iii) \(\frac{1}{4}\)
(iv) \(\frac{9}{64}\)
हल
(ii) \(\frac{1}{64}\)

प्रश्न 6.
द्विघात समीकरण 2x² – √5x + 1 = 0 के
(i) दो भिन्न वास्तविक मूल हैं
(ii) दो बराबर वास्तविक मूल हैं
(iii) कोई वास्तविक मूल नहीं है
(iv) दो से अधिक वास्तविक मूल हैं
हल
(iii) कोई वास्तविक मूल नहीं है

प्रश्न 7.
निम्नलिखित में से किस समीकरण के कोई वास्तविक मूल नहीं हैं?
(i) x² – 4x + 3√2 = 0
(ii) x² + 4x – 3√2 = 0
(iii) x² – 4x – 3√2 = 0
(iv) 3x² + 4√3x + 4 = 0
हल
(i) x² – 4x + 3√2 = 0

प्रश्न 8.
समीकरण (x² + 1)² – x² = 0
(i) के चार वास्तविक मूल हैं
(ii) के दो वास्तविक मूल हैं
(iii) के कोई वास्तविक मूल नहीं हैं
(iv) का एक वास्तविक मूल है
हल
(iii) के कोई वास्तविक मूल नहीं हैं

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
द्विघात समीकरण x² + kx + 3 = 0 का एक मूल 1 हो तो k का मान ज्ञात कीजिए।
हल
द्विघात समीकरण का एक मूल 1 है।
x = 1 द्विघात समीकरण को सन्तुष्ट करेगा।
द्विघात समीकरण में x = 1 रखने पर,
(1)² + k(1) + 3 = 0
⇒ k + 4 = 0
⇒ k = -4

प्रश्न 2.
समीकरण a²x² – 3abx + 2b² = 0 को हल कीजिए।
हल
दिया गया समीकरण a²x² – 3abx + 2b² = 0
⇒ a²x² – 2abx – abx + 2b² = 0
⇒ ax(ax – 2b) – b(ax – 2b) = 0
⇒ (ax – 2b) (ax – b) = 0
यदि (ax – 2b) = 0, तो x = \(\frac{2 b}{a}\)
और यदि (ax – b) = 0 , तो x = \(\frac{b}{a}\)
∴ x = \(\frac{2 b}{a}\), \(\frac{b}{a}\)

प्रश्न 3.
बिना हल किए b²x² + abx – a² = 0 के मूलों के लक्षण ज्ञात कीजिए।
हल
दिया गया समीकरण : b²x² + abx – a² = 0
उपर्युक्त समीकरण की तुलना मानक द्विघात समीकरण Ax² + Bx + C = 0 से करने पर,
A = b², B = ab, C = -a²
विविक्तकर, D = B² – 4AC
= (ab)² – 4b²(-a²)
= a²b² + 4a²b²
= 5a²b² > 0 परन्तु पूर्ण वर्ग नहीं है
अत: मूल वास्तविक, अपरिमेय और असमान होंगे।

प्रश्न 4.
p के वे मान ज्ञात कीजिए जिससे समीकरण 2px² – 8x + p = 0 के मूल बराबर व वास्तविक हों।
हल
दिया गया समीकरण : 2px² – 8x + p = 0
उपर्युक्त समीकरण की तुलना मानक द्विघात समीकरण, ax² + bx + c = 0 से करने पर,
a = 2p, b = -8, c = p
विविक्तकर, D = b² – 4ac
= (-8)² – 4 × 2p × p
= 64 – 8p²
मूल बराबर व वास्तविक हैं।
64 – 8p² = 0
⇒ p² = 8
⇒ p = ±2√2

प्रश्न 5.
सिद्ध कीजिए कि द्विघात समीकरण 3x² + 2√5x – 5 = 0 के मूल वास्तविक और असमान हैं। मूलों की प्रकृति भी ज्ञात कीजिए।
हल
दी गई समीकरण : 3x² + 2√5x – 5 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 3, b = 2√5 तथा c = -5
विविक्तिकर, D = b² – 4ac
= (2√5)² – 4 × 3 × (-5)
= 20 + 60
= 80 धनात्मक परन्तु पूर्ण वर्ग नहीं
अत: समीकरण के मूल वास्तविक, असमान व अपरिमेय होंगे।

प्रश्न 6.
द्विघात समीकरण 4x² – 8 = 0 के मूल ज्ञात कीजिए।
हल
4x² – 8 = 0
⇒ 4(x² – 2) = 0
⇒ (x + √2) (x – √2) = 0
x² – 2 = 0 होने के लिए, .
x + √2 = 0 ⇒ x = -√2
तथा x – √2 = 0 ⇒ x = √2
अत: द्विघात समीकरण के मूल -√2 तथा √2 हैं।

प्रश्न 7.
द्विघात समीकरण x² – 4x + 4 = 0 के मूलों की प्रकृति ज्ञात कीजिए।
हल
द्विघात समीकरण x² – 4x + 4 = 0 की तुलना द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 1, b = -4, c = 4
विविक्तकर, D = b² – 4ac
= (-4)² – 4 × 1 × 4
= 16 – 16
= 0
विविक्तकर, D का मान शून्य है।
अत: द्विघात समीकरण x² – 4x + 4 = 0 के मूल बराबर हैं।

प्रश्न 8.
जाँच कीजिए कि (x – 2)² + 1 = 2x + 3 द्विघात समीकरण है या नहीं।
हल
दी हुई समीकरण (x – 2)² + 1 = 2x + 3
⇒ x² – 4x + 4 + 1 = 2x + 3
⇒ x² – 4x – 2x + 5 – 3 = 0
⇒ x² – 6x + 2 = 0
यह समीकरण x में दो घात है तथा इनके गुणांक वास्तविक हैं।
अत: दी हुई समीकरण द्विघात समीकरण है।

प्रश्न 9.
द्विघात समीकरण 2x² – 4x + 3 = 0 का विविक्तकर ज्ञात कीजिए और मूलों की प्रकृति बताइए।
हल
दिया गया द्विघात समीकरण है :
2x² – 4x + 3 = 0
उपर्युक्त समीकरण की तुलना व्यापक द्विघात समीकरण ax² + bx + c = 0 से करने पर,
a = 2, b = -4, c = 3
विविक्तकर, D = b² – 4ac
= (-4)² – 4(2)(3)
= 16 – 24
= -8 (ऋणात्मक)
विविक्तकर ऋणात्मक है।
समीकरण के मूल अधिकल्पित हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
राम की आयु श्याम की आयु के वर्ग की पाँच गुनी है। यदि दोनों की आयु का अन्तर 18 वर्ष हो तो उनकी आयु अलग-अलग ज्ञात कीजिए।
हल
माना श्याम की आयु x वर्ष तथा राम की आयु y वर्ष है।
राम की आयु श्याम की आयु के वर्ग की पाँच गुनी है।
y = 5x² ……..(1)
दोनों की आयु का अन्तर 18 वर्ष है।
y – x = 18 …….(2)
समीकरण (1) से y का मान समीकरण (2) में रखने पर,
5x² – x = 18
⇒ 5x² – x – 18 = 0
⇒ 5x² – (10 – 9)x – 18 = 0
⇒ 5x² – 10x + 9x – 18 = 0
⇒ 5x(x – 2) + 9(x – 2) = 0
⇒ (x – 2) (5x + 9) = 0
⇒ (x – 2) (5x + 9) = 0 होगा यदि,
x – 2 = 0 ⇒ x = 2
5x + 9 = 0 ⇒ 5x = -9 ⇒ x = \(\frac{-9}{5}\) असम्भव
x = 2 वर्ष
x = 2 समीकरण (1) में रखने पर,
y = 5(2)² = 5 × 4 = 20
राम की आयु = 20 वर्ष तथा श्याम की आयु = 2 वर्ष।

प्रश्न 2.
‘a’ का मान ज्ञात कीजिए ताकि द्विघात समीकरण (a – 12)x² + 2(a – 12)x + 2 = 0 के मूल समान हों।
हल
द्विघात समीकरण Ax² + Bx + C = 0 के मूल समान हों तो B² – 4AC = 0
द्विघात समीकरण Ax² + Bx + C = 0 की तुलना दी हुई द्विघात समीकरण (a – 12)x² + 2(a – 12)x + 2 = 0 से करने पर,
A = (a – 12), B = 2(a – 12), C = 2
B² – 4AC = 0 से,
⇒ [2(a – 12)]² – 4 × (a – 12) × 2 = 0
⇒ 4(a – 12)(a – 12 – 2) = 0
⇒ (a – 12)(a – 14) = 0
⇒ (a – 12)(a – 14) = 0 होने के लिए,
a – 12 = 0 ⇒ a = 12 असम्भव
तथा a – 14 = 0 ⇒ a = 14

प्रश्न 3.
हंसों की एक टोली में से हंसों की कुल संख्या के वर्गमूल के \(\frac{7}{2}\) गुना हंस तालाब के किनारे खेल रहे हैं। यदि शेष 2 हंस तालाब के पानी में स्नान कर रहे हैं तो हंसों की कुल संख्या ज्ञात कीजिए।
हल
माना हंसों की कुल संख्या x है।
तब, तालाब के किनारे खेलने वाले हंसों की संख्या = \(\frac {7}{2}\) × कुल संख्या का वर्गमूल
= \(\frac {1}{2}\) × √x
= \(\frac{7}{2} \sqrt{x}\)
शेष हंस जो पानी में स्नान कर रहे हैं = x – \(\frac{7}{2} \sqrt{x}\)
परन्तु पानी में स्नान करने वाले शेष हंसों की संख्या = 2
2 = x – \(\frac{7}{2} \sqrt{x}\) या \(\frac{7}{2} \sqrt{x}\) = x – 2
दोनों पक्षों का वर्ग करने पर,
\(\frac{49}{4}\) x = (x – 2)²
⇒ 49x = 4(x – 2)²
⇒ 49x = 4(x² – 4x + 4)
⇒ 49x = 4x² – 16x + 16
⇒ 4x² – 65x + 16 = 0
⇒ (4x – 1) (x – 16) = 0
⇒ (4x – 1)(x – 16) = 0 होगा यदि,
x – 16 = 0 ⇒ x = 16
तथा 4x – 1 = 0 ⇒ x = \(\frac{1}{4}\)
परन्तु हंसों की संख्या भिन्नात्मक नहीं हो सकती।
अत: हंसों की कुल संख्या = 16

प्रश्न 4.
किसी आयताकर मैदान का विकर्ण उसकी छोटी भुजा से 60 मी अधिक लम्बा है। यदि उसकी बड़ी भुजा छोटी भुजा से 30 मी अधिक हो, तो मैदान का परिमाप ज्ञात कीजिए।
हल
माना मैदान की छोटी भुजा = x मी
बड़ी भुजा = (x + 30) मी
तथा विकर्ण = (x + 60) मी
परन्तु (विकर्ण)² = (बड़ी भुजा)² + (छोटी भुजा)²
⇒ (x + 60)² = (x + 30)² + x²
⇒ x² + 3600 + 120x = x² + 900 + 60x + x²
⇒ x² – 60x – 2700 = 0
⇒ x² – 90x + 30x – 2700 = 0
⇒ x(x – 90) + 30(x – 90) = 0
⇒ (x – 90) (x + 30) = 0
⇒ x = 90 या -30 (मान्य नहीं)
मैदान की छोटी भुजा = 90 मी
तथा बड़ी भुजा = 90 + 30 = 120 मी
मैदान का परिमाप = 2(बड़ी भुजा + छोटी भुजा)
= 2(120 + 90)
= 420 मी

प्रश्न 5.
दो क्रमागत धन सम संख्याओं के वर्गों का योग 244 है। संख्याएँ ज्ञात कीजिए।
हल
माना दो क्रमागत धन सम संख्याएँ 2x व (2x + 2) हैं।
तब प्रश्नानुसार,
(2x)² + (2x + 2)² = 244
⇒ 4x² + 4x² + 4 + 8x = 244
⇒ 8x² + 8x – 240 = 0
⇒ x² + x – 30 = 0
⇒ x² + 6x – 5x – 30 = 0
⇒ x(x + 6) – 5(x + 6) = 0
⇒ (x + 6) (x – 5) = 0
यदि x + 6 = 0 तो x = -6 जोकि मान्य नहीं है।
यदि x – 5 = 0 तो x = 5
धन सम संख्याएँ क्रमश:
2 × 5 = 10 व 10 + 2 = 12 हैं।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
पूर्ण वर्ग बनाने की विधि से समीकरण 5x² – 6x – 2 = 0 के मूल ज्ञात कीजिए।
हल
दिया गया समीकरण है : 5x² – 6x – 2 = 0

प्रश्न 2.
ऊँटों के झुण्ड का एक-चौथाई जंगल में देखा जाता है। झुण्ड के वर्गमूल का दोगुना पहाड़ी पर चला गया और शेष 15 ऊँटों को एक नदी के किनारे देखा जाता है। ऊँटों की कुल संख्या ज्ञात कीजिए।
हल
माना झुण्ड के कुल ऊँटों की संख्या x है।
तब, प्रश्नानुसार जंगल में गए ऊँटों की संख्या = \(\frac{x}{4}\)
तथा पहाड़ी पर गए ऊँटों की संख्या = 2√x
शेष ऊँटों की संख्या = x – \(\frac{x}{4}\) – 2√x = \(\frac{3 x}{4}\) – 2√x
परन्तु प्रश्नानुसार शेष ऊँटों की संख्या 15 है।
\(\frac{3 x}{4}\) – 2√x = 15
⇒ \(\frac{3 x}{4}\) – 15 = 2√x
⇒ \(\frac{3 x-60}{4}\) = 2√x
⇒ 3x – 60 = 8√x
⇒ (3x – 60)² = (8√x)² |दोनों पक्षों का वर्ग करने पर]
⇒ 9x² – 360x + 3600 = 64x
⇒ 9x² – 360x + 3600 – 64x = 0
⇒ 9x² – 424x + 3600 = 0
⇒ 9x² – (324 + 100)x + 3600 = 0
⇒ 9x² – 324x – 100x + 3600 = 0
⇒ 9x(x – 36) – 100(x – 36) = 0
⇒ (9x – 100)(x – 36) = 0
तब, (9x – 100) अथवा (x – 36) में से एक शून्य अवश्य होगा।
अब यदि 9x – 100 = 0 हो, तो x = \(\frac{100}{9}\) (एक भिन्नात्मक संख्या)
ऊँटों की संख्या पूर्ण ही हो सकती है, भिन्नात्मक नहीं; अत: x का मान \(\frac{100}{9}\) स्वीकार्य नहीं है।
तब, x – 36 का मान शून्य अवश्य होगा, अर्थात्
x – 36 = 0 ⇒ x = 36
अतः झुण्ड में ऊँटों की संख्या = 36

प्रश्न 3.
निम्नलिखित समीकरण को द्विघात समीकरण में समानीत करके हल कीजिए
\(8\left(x^{2}+\frac{1}{x^{2}}\right)-42\left(x-\frac{1}{x}\right)+29=0\)
हल
दिया गया समीकरण
\(8\left(x^{2}+\frac{1}{x^{2}}\right)-42\left(x-\frac{1}{x}\right)+29=0\)

प्रश्न 4.
मुम्बई से पूना तक की 192 किमी की दूरी तय करने में एक तेज चलने वाली गाड़ी, धीरे चलने वाली गाड़ी से 2 घण्टा कम समय लेती है। यदि धीरे चलने वाली गाड़ी की औसत चाल तेज चलने वाली गाड़ी की औसत चाल से 16 किमी/घण्टा कम हो, तो प्रत्येक गाड़ी की औसत चाल ज्ञात कीजिए।
हल
माना तेज चलने वाली गाड़ी की औसत चाल = x किमी/घण्टा
धीरे चलने वाली गाड़ी की औसत चाल = (x – 16) किमी/घण्टा
तेज चलने वाली गाड़ी द्वारा 192 किमी दूरी तय करने में लगा समय = \(\frac{192}{x}\) घण्टा
धीरे चलने वाली गाड़ी द्वारा 192 किमी दूरी तय करने में लगा समय = \(\frac{192}{x-16}\) घण्टा

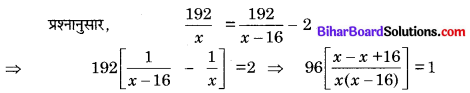
⇒ x² – 16x = 96 × 16
⇒ x² – 16x – 1536 = 0
⇒ x² – 48x + 32x – 1536 = 0
⇒ x(x – 48) + 32(x – 48) = 0
⇒ (x – 48)(x + 32) = 0
यदि x – 48 = 0, तो x = 48
और यदि x + 32 = 0, तो x = -32 जो अग्राह्य है।
अत: x = 48 किमी/घण्टा
अत: तेज चलने वाली गाड़ी की औसत चाल = 48 किमी/घण्टा
तथा धीरे चलने वाली गाड़ी की औसत चाल = 48 – 16 = 32 किमी/घण्टा

प्रश्न 5.
एक नाव को जिसकी शान्त जल में चाल 15 किमी/घण्टा है, धारा की दिशा में 30 किमी जाने और फिर धारा के विपरीत दिशा में लौटने में कुल 4 घण्टा 30 मिनट लगता है। धारा की चाल ज्ञात कीजिए।
हल
शान्त जल में नाव की चाल = 15 किमी/घण्टा
माना, नदी की चाल = x किमी/घण्टा
धारा के अनुकूल नाव की चाल = (15 + x) किमी/घण्टा
धारा के विपरीत नाव की चाल = (15 – x) किमी/घण्टा
धारा के अनुकूल 30 किमी जाने में लगा समय = \(\left(\frac{30}{15+x}\right)\) घंटा
धारा के विपरीत 30 किमी जाने में लगा समय = \(\left(\frac{30}{15-x}\right)\) घंटा

⇒ 225 – x² = 200
⇒ x² = 225 – 200
⇒ x² = 25
⇒ x = ±5
परन्तु x ≠ -5, चूँकि चाल ऋणात्मक नहीं हो सकती।
अत: x = 5
अतः धारा की चाल 5 किमी/घण्टा है।