Bihar Board Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.5 Text Book Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.5
Bihar Board Class 10 Maths त्रिभुज Ex 6.5
प्रश्न 1.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लम्बाई भी खिए।
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
हल
समकोण त्रिभुजों में सबसे लम्बी भुजा कर्ण का वर्ग शेष दोनों भुजाओं के वर्गों के योग के बराबर होता है।
(i) माना a = 7 cm, b = 24 cm तथा c = 25 cm
तब, (सबसे लम्बी भुजा)2 = c2 = (25)2 = 625
तथा a2 + b2 = (7)2 + (24)2 = 49 + 576 = 625
c2 = a2 + b2 अर्थात् सबसे लम्बी भुजा का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर है।
अत: दिया गया त्रिभुज समकोण त्रिभुज है। कर्ण की लम्बाई = 25 सेमी।
(ii) माना a = 3 cm, b = 8 cm तथा c = 6 cm,
तब, b2 = (8)2 = 64
तथा a2 + c2 = 32 + 62 = 9 + 36 = 45
b2 ≠ c2 + a2 अर्थात् सबसे लम्बी भुजा का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर नहीं है।
अत: दिया गया त्रिभुज समकोण त्रिभुज नहीं है।
![]()
(iii) माना a = 50 cm, b = 80 cm तथा c = 100 cm
तब, c2 = (100)2 = 10,000
तथा a2 + b2 = (50)2 + (80)2 = 2500 + 6400 = 8900
c2 ≠ a2 + b2 अर्थात् सबसे लम्बी भुजा का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर नहीं है।
अतः दिया गया त्रिभुज समकोण त्रिभुज नहीं है।
(iv) माना a = 13 cm, b = 12 cm तथा c = 5 cm
तब, a2 = (13)2 = 169
तथा b2 + c2 = (12)2 + (5)2 = 144 + 25 = 169
a2 = b2 + c2 अर्थात् सबसे लम्बी भुजा का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर है।
अत: दिया गया त्रिभुज समकोण त्रिभुज है।
कर्ण की लम्बाई = 13 सेमी।
![]()
प्रश्न 2.
PQR एक समकोण त्रिभुज है जिसका कोण Pसमकोण है तथा QR पर बिन्दु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM2 = QM . MR है।
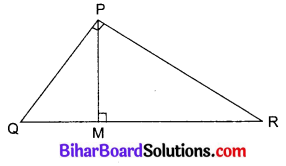
हल
दिया है : समकोण त्रिभुज PQR में ∠P समकोण है तथा PM ⊥ QR है।
सिद्ध करना है : PM2 = QM . MR
उपपत्ति : :: समकोण त्रिभुज PQR में ∠P समकोण है और इसके समकोण वाले शीर्ष P से कर्ण QR पर लम्ब खींचा गया है।
∆PQM ~ ∆RPM
\(\frac{Q M}{P M}=\frac{P M}{M R}\) (:: ∆PQM और ∆PRM की भुजाएँ आनुपातिक हैं)
PM2 = QM . MR (वज्रगुणन से)
अतः PM2 = QM . MR
इति सिद्धम्
प्रश्न 3.
दी गई आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि-
(i) AB2 = BC . BD
(ii) AC2 = BC . DC
(iii) AD2 = BD . CD
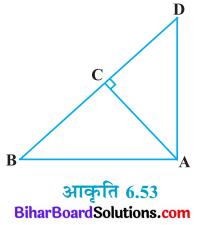
हल
दिया है : ΔABD में ∠DAB = 90° तथा AC ⊥ BD
सिद्ध करना है :
(i) AB2 = BC . BD
(ii) AC2 = BC . DC
(iii) AD2 = BD . CD
उपपत्ति : ΔABD में, ∠DAB = 90°
ΔABD समकोण त्रिभुज है जिसमें AC ⊥ BD
ΔABC ~ ΔDBA और ΔDAC ~ ΔDBA तथा ΔABC ~ ΔDAC
(i) ∵ ΔABC ~ ΔDBA
∴ ΔABC तथा ΔDBA की तुलना करने पर,
\(\frac{B C}{A B}=\frac{A B}{B D}\)
AB2 = BC . BD
इति सिद्धम्
(ii) ∵ ΔABC ~ ΔDAC
∴ ΔABC तथा ΔDAC की तुलना करने पर,
\(\frac{B C}{A C}=\frac{A C}{D C}\)
AC2 = BC · DC
इति सिद्धम्
(iii) ∵ ΔDAC ~ ΔDBA
∴ ΔDAC तथा ΔDBA की तुलना करने पर,
\(\frac{A D}{B D}=\frac{C D}{A D}\)
AD2 = BD . CD
इति सिद्धम्
![]()
प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
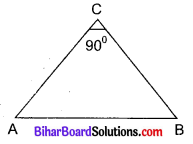
हल
दिया है : ΔABC समद्विबाहु है जिसमें ∠C = 90° तथा BC = AC
सिद्ध करना है : AB2 = 2AC2
उपपत्ति : समद्विबाहु समकोण ΔABC में,
पाइथागोरस प्रमेय के अनुसार,
AB2 = AC2 + BC2
⇒ AB2 = AC2 + (AC)2
⇒ AB2 = AC2 + AC2 [∵ दिया है, BC = AC]
अत : AB2 = 2AC2
इति सिद्धम्
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। यदि AB2 = 2AC2 हो तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
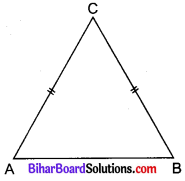
हल
दिया है : समद्विबाहु ΔABC में,
AC = BC और AB2 = 2AC2
सिद्ध करना है : ΔABC एक समकोण त्रिभुज है।
उपपत्ति : AB2 = 2AC2
⇒ AB2 = AC2 + AC2
⇒ AB2 = BC2 + AC2 (∵ AC = BC)
पाइथागोरस प्रमेय के विलोम से, ΔABC समकोण त्रिभुज होगा।
इति सिद्धम्
![]()
प्रश्न 6.
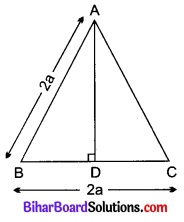
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलम्ब की लम्बाई ज्ञात कीजिए।
हल
ΔABC समबाहु त्रिभुज है।
त्रिभुज की भुजा AB = 2a, BC = 2a तथा CA = 2a
त्रिभुज के शीर्ष A से BC पर लम्ब AD खींचा गया है।
BD = \(\frac{1}{2}\) BC
⇒ BD = \(\frac{1}{2}\) (2a) = a
तब, समकोण त्रिभुज ABD में,
AD2 + BD2 = AB2
⇒ AD2 + a2 = (2a)2
⇒ AD2 = 4a2 – a2 = 3a2
⇒ AD = a√3
शीर्षलम्ब, AD = a√3
त्रिभुज समबाहु है; अत: दो अन्य शीर्षलम्बों की लम्बाई भी a√3 होगी।
प्रश्न 7.
सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग विकर्णों के योग के बराबर होता है।
हल
दिया है : चतुर्भुज ABCD एक समचतुर्भुज है जिसमें AC तथा CD दो विकर्ण हैं जो परस्पर O पर काटते हैं।
सिद्ध करना है : AB2 + BC2 + CD2 + DA2 = AC2 + BD2


![]()
प्रश्न 8.
दी गई आकृति में ∆ABC के अभ्यन्तर में स्थित कोई बिन्दु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि-
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
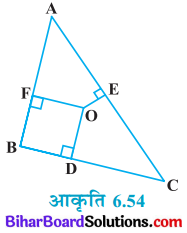
हल
दिया है : ∆ABC के अन्दर एक बिन्दु O है जिससे भुजाओं BC, CA तथाAD पर क्रमशः OD, OE और OF लम्ब खींचे गए हैं।
सिद्ध करना है :
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
रचना : रेखाखण्ड OA, OB तथा OC खींचिए।
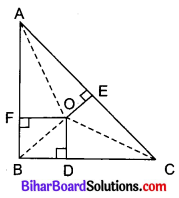
उपपत्ति :
(i) समकोण ∆OAF में,
AF2 + OF2 = OA2 ……(1)
समकोण ∆OBD में,
BD2 + OD2 = OB2 ……..(2)
समकोण ∆OCE में,
CE2 + OE2 = OC2 ……(3)
समीकरण (1), समीकरण (2) और समीकरण (3) को जोड़ने पर,
AF2 + BD2 + CE2 + OF2 +OD2 + OE2 = OA2 + OB2 + OC2
अत: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 – OD2 – OE2 – OF2
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
इति सिद्धम्
(ii) समकोण ∆OBD में,
OD2 + BD2 = OB2 ……(4)
समकोण ∆OCD में,
OD2 + CD2 = OC2 …….(5)
समीकरण (5) को समीकरण (4) में से घटाने पर,
BD2 – CD2 = OB2 – OC2 …..(6)
इसी प्रकार, समकोण ∆OCE व ∆OAE में,
CE2 – AE2 = OC2 – OA2 …….(7)
और समकोण ∆OAF व ∆OBF में,
AF2 – BF2 = OA2 – OB2 ……(8)
अब, समीकरण (6), समीकरण (7) और समीकरण (8) को जोड़ने पर,
BD2 + CE2 + AF2 – CD2 – AE2 – BF2 = 0
अतः AF2 + BD2 + CE2 = AE2 + CD2 + BF2
इति सिद्धम्
प्रश्न 9.
10 m लम्बी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुंचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
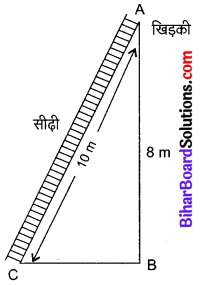
हल
दिया है : भूमि से 8 m ऊँचाई पर एक खिड़की A है जिससे खिड़की AB = 8 m सीढ़ी की लम्बाई AC = 10 m है जिसे खिड़की से लगाने पर उसका निचला सिरा भूमि पर बिन्दु C पर पड़ता है।
ज्ञात करना है : दीवार के आधार से सीढ़ी के निचले सिरे की दूरी BC
गणना : समकोण त्रिभुज ABC में,
AB2 + BC2 = AC2
⇒ (8)2 + (BC)2 = (10)2
⇒ 64 + BC2 = 100
⇒ BC2 = 100 – 64 = 36
⇒ BC2 = 36
⇒ BC = √36 = 6 m
अतः दीवार के आधार से सीढ़ी के निचले सिरे की दूरी (BC) = 6 m
![]()
प्रश्न 10.
18 m ऊँचे एक ऊर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूटे से जुड़ा हुआ है। खम्भे के आधार से खुंटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लम्बाई 24 m है।
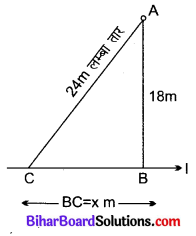
हल
दिया है : माना क्षैतिज धरातल पर l एक सरल रेखा है जिसके किसी बिन्दु B पर एक खम्भा AB ऊर्ध्वाधर गड़ा है। एक तार जिसकी लम्बाई 24 m है, का एक सिरा खम्भे के शिखर A से बँधा है। तार का दूसरा सिरा धरातल पर गड़े एक खूटे C से बँधा है। तार तना रहता है।
ज्ञात करना है : खम्भे के सिरे B की खूटे C से दूरी BC
विश्लेषण : माना खम्भे के आधार B से खूटे की दूरी BC = x m है।
खम्भा भूमि पर सीधा गड़ा है।
∠ABC = 90°
∆ABC समकोणीय है।
पाइथागोरस प्रमेय से,
AB2 + BC2 = CA2
⇒ 182 + x2 = 242
⇒ x2 = 242 – 182 = 576 – 324 = 252
⇒ x = √252 = \(\sqrt{6 \times 6 \times 7}\)
⇒ x = 6√7
अत: खम्भे के आधार से खूटे की दूरी x = 6√7 मीटर या 15.87 मीटर।
प्रश्न 11.
एक हवाईजहाज एक हवाई अड्डे से उत्तर की ओर 1000 किमी प्रति घण्टा की चाल से उड़ता है। इसी समय एक अन्य हवाईजहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 किमी प्रति घण्टा की चाल से उड़ता है। 1\(\frac{1}{2}\) घण्टे के बाद दोनों हवाईजहाजों के बीच की दूरी कितनी होगी?
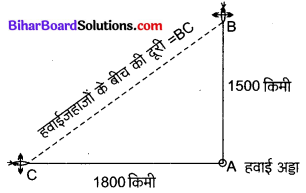
हल
पहले हवाई जहाज द्वारा हवाई अड्डे A से उत्तर दिशा में 1\(\frac{1}{2}\) घण्टे में चली गई दूरी,
AB = 1000 × 1\(\frac{1}{2}\)
= 1000 × \(\frac{3}{2}\)
= 1500 किमी
दूसरे हवाई जहाज द्वारा हवाई अड्डे A से पश्चिम दिशा में 1\(\frac{1}{2}\) घण्टे में चली गई दूरी,
AC = 1200 × 1\(\frac{1}{2}\)
= 1200 × \(\frac{3}{2}\)
= 1800 किमी
तब, समकोण त्रिभुज ABC में,
BC2 = AB2 + AC2
⇒ BC2 = (1500)2 + (1800)2
⇒ BC2 = 2250000 + 3240000
⇒ BC2 = 5490000
⇒ BC2 = 9 × 10000 × 61
⇒ BC = \(\sqrt{9 \times 10000 \times 61}\) = 300√61 किमी
अत: 1\(\frac{1}{2}\) घण्टे बाद दोनों हवाईजहाजों के बीच की दूरी = 300√61 किमी
![]()
प्रश्न 12.
दो खम्भे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके निचले सिरों के बीच की दूरी 12 m हो तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
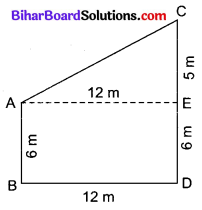
हल
दिया है : AB = 6 m तथा CD = 11 m लम्बाई के दो खम्भे मैदान में खड़े हैं जिनके निचले सिरों B और D के बीच की दूरी BD = 12 m है।
ज्ञात करना है : ऊपरी सिरों के बीच की दूरी AC
रचना : A से CD पर लम्ब AE खींचा।
गणना : AB = 6 m, CD = 11 m, BD = 12 m
∴ AE = 12 m तथा ED = AB = 6 m
∵ CD = 11 m
CE + ED = 11 m
⇒ CE + 6 = 11 m
⇒ CE = 11 – 6 = 5 m
समकोण ∆ACE में,
AC2 = AE2 + CE2 = (12)2 + (5)2 = 144 + 25 = 169
⇒ AC = √169 = 13 m
अत: दोनों ऊपरी सिरों के बीच की दूरी AC = 13 m
प्रश्न 13.
एक ∆ABC जिसका ∠C समकोण है की भुजाओं CA और CB पर क्रमशः बिन्दु D और E पर स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2 है।
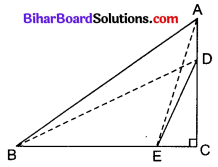
हल
दिया है : समकोण त्रिभुज ABC जिसमें ∠C समकोण है। बिन्दु D और E क्रमशः भुजाओं CA व CB पर स्थित हैं।
सिद्ध करना है : AE2 + BD2 = AB2 + DE2
उपपत्ति : समकोण त्रिभुज ABC में,
AC2 + BC2 = AB2 …….(1)
और समकोण त्रिभुज DEC में,
CD2 + CE2 = DE2 …….(2)
समीकरण (1) व (2) को जोड़ने पर,
AB2 + DE2 = AC2 + BC2 + CD2 + CE2 …..(3)
समकोण त्रिभुज DBC में, BD2 = BC2 + CD2 ……..(4)
समकोण त्रिभुज AEC में, AE2 = AC2 + CE2 ……(5)
समीकरण (4) व (5) को जोड़ने पर,
AE2 + BD2 = AC2 + BC2 + CE2 + CD2
समीकरण (3) व (6) से, AE2 + BD2 = AB2 + DE2
इति सिद्धम्
![]()
प्रश्न 14.
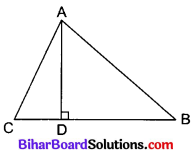
किसी ∆ABC के शीर्ष A से भुजा BC पर डाला गया लम्ब BC को बिन्दु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है। सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
हल
दिया है : ∆ABC में आधार BC पर शीर्ष A से AD लम्ब इस प्रकार डाला गया है कि BD = 3CD
सिद्ध करना है : 2AB2 = 2AC2 + BC2
उपपत्ति : समकोण त्रिभुज ABD में,
AB2 = AD2 + BD2
दोनों पक्षों में 2 से गुणा करने पर,
2AB2 = 2AD2 + 2BD2
⇒ 2AB2 = 2 AC2 – CD2 + 2(3CD)2 (∵ AD2 = AC2 – CD2; BD = 3CD)
⇒ 2AB2 = 2AC2 – 2CD2 + 18CD2
⇒ 2AB2 = 2AC2 + 16CD2
⇒ 2AB2 = 2AC2 + (4CD)2
⇒ 2AB2 = 2AC2 + (CD + 3CD)2
⇒ 2AB2 = 2AC2 + (CD + BD)2 (∵ 3CD = BD)
⇒ 2AB2 = 2AC2 + BC2 (∵ BC = CD + BD)
अतः 2AB2 = 2AC2 + BC2
इति सिद्धम्
प्रश्न 15.
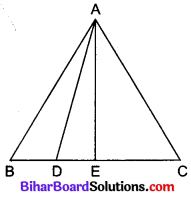
किसी समबाहु त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार स्थित है कि BD = \(\frac{1}{3}\) BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
हल
दिया है : ∆ABC एक समबाहु त्रिभुज है जिसके आधार BC पर एक बिन्दु D इस प्रकार है कि BD = \(\frac{1}{3}\) BC
सिद्ध करना है : 9AD2 = 7AB2
रचना : A से BC पर AE लम्ब खींचिए।
उपपत्ति : समबाहु ∆ABC में, AE ⊥ BC
BE = CE = \(\frac{1}{2}\) BC
BE = \(\frac{1}{2}\)AB (∵ BC = AB) …..(1)
समकोण ∆ABE में,


दोनों पक्षों में लघुत्तम समापवर्त्य 36 से गुणा करने पर,
36 × (\(\frac{3}{4}\) AB2) + 36 × (\(\frac{1}{36}\) AB2) = 36AD2
⇒ 27AB2 + AB2 = 36AD2
⇒ 28AB2 = 36AD2
⇒ 7AB2 = 9AD2 (4 सार्वनिष्ठ है)
अतः 9AD2 = 7AB2
इति सिद्धम्
![]()
प्रश्न 16.
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलम्ब के वर्ग के चार गुने के बराबर होता है।
हल
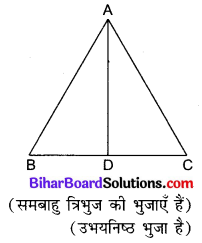
दिया है : ABC एक समबाहु त्रिभुज है जिसकी एक भुजा AB है।
त्रिभुज के शीर्ष A से आधार BC तक शीर्ष लम्ब AD खींचा गया है।
सिद्ध करना है : भुजा2 × 3 = शीर्ष लम्ब2 × 4 अर्थात्
अर्थात 3AB2 = 4AD2
उपपत्ति : माना AB = 2a
⇒ a = \(\frac{1}{2}\) AB
∆ABC समबाहु है,
AB = BC
⇒ BC = 2a
शीर्ष A से BC पर AD लम्ब है।
समकोण ∆ABD तथा ∆ACD में,
AB = AC (समबाहु त्रिभुज की भुजाएँ हैं)
AD = AD (उभयनिष्ठ भुजा है)
∆ABD ≅ ∆ACD
BD = CD = CD
परन्तु BC = BD + CD = 2a
⇒ BD = a
तब, समकोण ∆ABD में,
AB2 = BD2 + AD2
⇒ (2a)2 = (a)2 + AD2
⇒ AD2 = 4a2 – a2 = 3a2
⇒ AD2 = 3 × \(\left(\frac{A B}{2}\right)^{2}\) (∵ a = \(\frac{1}{2}\) AB)
⇒ AD2 = \(\frac{3 A B^{2}}{4}\)
अत: 3AB2 = 4AD2
अथवा भुजा2 × 3 = शीर्षलम्ब2 × 4
इति सिद्धम्
![]()
प्रश्न 17.
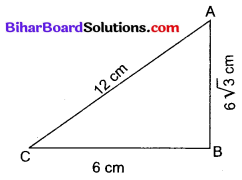
सही उत्तर चुनकर उसका औचित्य दीजिए : ∆ABC में, AB = 6√3 cm, AC = 12 cm और BC = 6 cm है। कोण B है-
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल
∆ABC में, AB = 6√3 cm, AC = 12 cm और BC = 6 cm
AB = 6√3 cm
⇒ AB2 = (6√3)2 = 36 × 3 = 108
BC = 6 cm
⇒ BC2 = (6)2 = 36
तथा AC = 12 cm
⇒ AC2 = (12)2 = 144
तब, AB2 + BC2 =108 + 36 = 144
और AC2 = 144
∴ AB2 + BC2 = AC2
∴ त्रिभुज ABC समकोणीय है जिसमें कर्ण AC है।
तथा ∠B समकोण है।
∠B = 90°
अत: विकल्प (C) सही है।