Bihar Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 Text Book Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4
Bihar Board Class 10 Maths त्रिकोणमिति का परिचय Ex 8.4
प्रश्न 1.
त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए
हल
हम जानते हैं कि cot A और cosec A में सम्बन्ध ‘cosec2 A = 1 + cot2 A’ है और cosec A और sin A में सम्बन्ध प्रतिलोम का है।
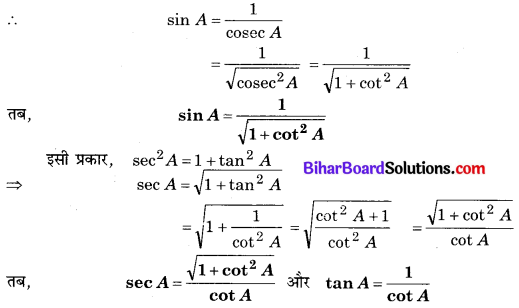
![]()
प्रश्न 2.
∠A के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
हल


![]()
प्रश्न 3.
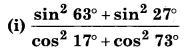
(ii) sin 25° cos 65° + cos 25° sin 65°
हल
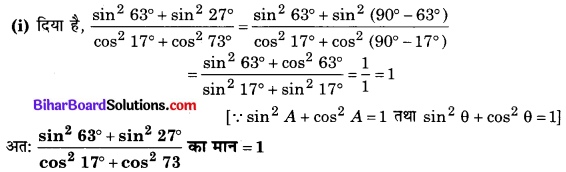
(ii) दिया है, sin 25° cos 65° + cos 25° sin 65°
= sin 25° cos (90° – 25°) + cos 25° sin (90° – 25°)
= sin 25° sin 25° + cos 25° cos 25°
[∵ cos (90° – 25°) = sin 25° तथा sin(90° – 25°) = cos 25°]
= sin2 25° + cos2 25°
= 1 [∵ sin2 A+ cos2 A = 1]
अतः sin 25° cos 65° + cos 25° sin 65° = 1
![]()
प्रश्न 4.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए-
(i) 9 sec2 A – 9 tan2 A बराबर है-
(A) 1
(B) 9
(C) 8
(C) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) बराबर है-
(A) 0
(B) 1
(C) 2
(D) -1
(iii) (sec A + tan A)(1 – sin A) बराबर है-
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) बराबर है-
(A) sec2 A
(B) -1
(C) cot2 A
(D) tan2 A
हल
(i) यहाँ 9 sec2 A – 9 tan2 A
= 9 (sec2 A – tan2 A)
= 9 (1 + tan2 A – tan2 A) [∵ sec2 A = 1 + tan2 A]
= 9 × (1)
= 9
अत: विकल्प (B) सही है।
(ii) यहाँ (1 + tan θ + sec θ) (1 + cot θ – cosec θ)


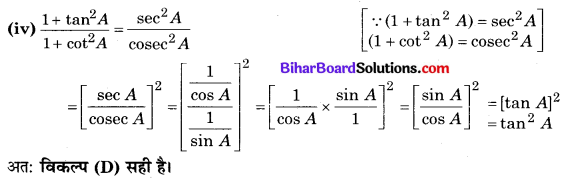
![]()
प्रश्न 5.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यूनकोण हैं-

हल










