Bihar Board Class 10 Maths Solutions Chapter 10 वृत्त Ex 10.2 Text Book Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 10 वृत्त Ex 10.2
Bihar Board Class 10 Maths वृत्त Ex 10.2
प्रश्न सं० 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।
प्रश्न 1.
एक बिन्दु से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केन्द्र से दूरी 25 cm है। वृत्त की त्रिज्या है :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
हल
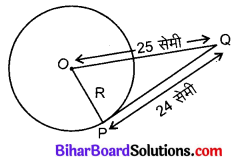
माना वृत्त की त्रिज्या R cm है।
दिया है, स्पर्श रेखा की लम्बाई (PQ) = 24 cm
और बिन्दु Q से वृत्त के केन्द्र की दूरी (OP) = 25 cm
समकोण ΔOPQ में, पाइथागोरस प्रमेय से,
OQ2 = OP2 + PQ2
⇒ OP2 = OQ2 – PQ2
⇒ R2 = (25)2 – (24)2
⇒ R2 = 625 – 576
⇒ R2 = 49
⇒ R = 7
अत: विकल्प (A) सही है।
![]()
प्रश्न 2.
आकृति में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर है-
(A) 60°
(B) 70°
(C) 80°
(D) 90°
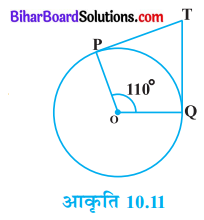
हल
दिया है, दिए हुए वृत्त में OP तथा OQ त्रिज्याएँ हैं और TP तथा TQ स्पर्श रेखाएँ हैं।
तथा ∠POQ = 110°
∵ OP ⊥ PT तथा OQ ⊥ QT
∴ ∠P = 90° तथा ∠Q = 90°
चतुर्भुज OPTQ में,
∠POQ + ∠PTQ = 180°
या 110° + ∠PTQ = 180°
या ∠PTQ = 180° – 110° = 70°
अत: विकल्प (B) सही है।
प्रश्न 3.
यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों तो ∠POA बराबर है-
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल
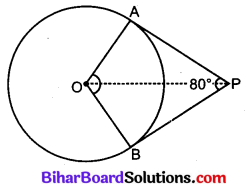
वृत्त का केन्द्र O है और बिन्दु P से PA व PB वृत्त पर स्पर्श रेखाएँ हैं जिनके बीच का कोण ∠APB = 80°
∵ ∠A = 90° व ∠B = 90°
⇒ ∠AOB व ∠APB सम्पूरक हैं।
∴ ∠AOB + ∠APB = 180° ……(1)
समीकरण (1) में ∠APB = 80° रखने पर,
∠AOB + 80° = 180°
⇒ ∠AOB = 100°
रेखा OP, ∠AOB को समद्धिभाजित करती है,
∠POB = \(\frac {1}{2}\) ∠AOB = \(\frac {1}{2}\) × 100° = 50°
अत: विकल्प (A) सही है।
![]()
प्रश्न 4.
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
हल
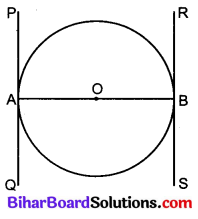
दिया है : एक वृत्त का केन्द्र O तथा व्यास AB है। व्यास के सिरों A तथा B से वृत्त पर स्पर्श रेखाएँ PAQ तथा RBS खींची गई हैं।
सिद्ध करना है : PQ || RS
उपपत्ति : दिया है, AB वृत्त का व्यास है और PAQ तथा RBS बिन्दुओं A तथा B पर वृत्त की स्पर्श रेखाएँ हैं।
∴ ∠PAB = 90° तथा ∠ABS = 90°
परन्तु ∠PAB तथा ∠ABS ऋजु रेखाओं PQ तथा RS को तिर्यक रेखा AB के द्वारा काटने से बने समान एकान्तर कोण हैं।
PQ || RS
इति सिद्धम्
प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
हल
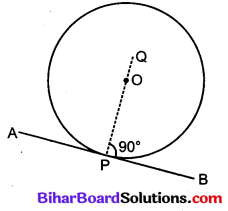
दिया है : एक वृत्त का केन्द्र O है और AB वृत्त की स्पर्श रेखा है जो वृत्त को बिन्दु P पर स्पर्श करती है।
P से वृत्त की स्पर्श रेखा AB पर PQ लम्ब खींचा गया है।
सिद्ध करना है : लम्ब PQ वृत्त के केन्द्र O से जाता है।
उपपत्ति: ∵ AP,वृत्त के स्पर्श बिन्दु P पर स्पर्श-रेखा है।
∴ AP, वृत्त की त्रिज्या पर लम्ब होगी।
∵ PQ ⊥ AP
∴ PQ रेखा में वृत्त की त्रिज्या समाहित होगी।
∵ त्रिज्या का एक सिरा P है, तब दूसरा सिरा केन्द्र O होगा।
∴ रेखा PQ में केन्द्र O भी समाहित है।
अतः लम्ब PQ वृत्त के केन्द्र O से होकर जाता है।
इति सिद्धम्
![]()
प्रश्न 6.
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल
बिन्दु A से वृत्त के केन्द्र की दूरी (D) = 5 cm
और वृत्त की स्पर्श रेखा की लम्बाई (T) = 4 cm
माना वृत्त की त्रिज्या R cm है।
∵ बिन्दु A से,
(वृत्त की स्पर्श रेखा की लम्बाई)2 = (वृत्त के केन्द्र से दूरी)2 – (त्रिज्या)2
⇒ T2 = D2 – R2
⇒ (4)2 = (5)2 – R2
⇒ R2 = 52 – 42 = 25 – 16 = 9
⇒ R = 3 cm
अत: वृत्त की त्रिज्या (R) = 3 cm
प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल
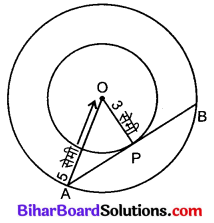
माना O केन्द्र वाले दो संकेन्द्रीय वृत्त हैं जिनकी त्रिज्याएँ OA तथा OP क्रमश: 5 cm व 3 cm हैं।
बड़े वृत्त की एक जीवा AB है जो छोटे वृत्त को बिन्दु P पर स्पर्श करती है।
∴ OP ⊥ AB (OP वृत्त की त्रिज्या है)
∴ ∆OAP समकोणीय त्रिभुज है।
तब, पाइथागोरस प्रमेय से,
AP2 + OP2 = OA2
⇒ AP2 + (3)2 = (5)2
⇒ AP2 = (5)2 – (3)2 = 25 – 9 = 16
⇒ AP = 4 cm
परन्तु बड़े वृत्त में, जीवा AB पर केन्द्र O से OP लम्ब है।
∴ P, AB को अर्धित करता है
∴ AP = BP
⇒ BP = 4 cm
तब, जीवा AB की लम्बाई = AP + BP = 4 + 4 = 8 cm
![]()
प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। सिद्ध कीजिए-
AB + CD = AD + BC
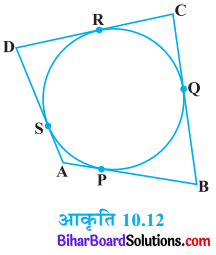
हल
दिया है : O केन्द्र वाले वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है जिसकी भुजाएँ AB, BC, CD तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R और S पर स्पर्श करती हैं।
सिद्ध करना है : AB + CD = AD + BC
उपपत्ति: ∴ AB तथा AD वृत्त को P तथा S पर स्पर्श करती हैं।
AP= AS
पुन: AB तथा BC वृत्त को P तथा Q पर स्पर्श करती हैं।
∴ PB = BQ
∵ BC तथा CD वृत्त को Q तथा R पर स्पर्श करती हैं।
∴ QC = CR
और CD तथा DA वृत्त को R तथा S पर स्पर्श करती हैं।
∴ DR = SD
AB + CD = AP + PB + DR + CR (आकृति देखिए)
= AS + BQ + SD + QC
= (AS + SD) + (BQ + QC)
= AD + BC
अत: AB + CD = AD + BC
इति सिद्धम्
प्रश्न 9.
संलग्न आकृति में, XY और X’Y’, O केन्द्र के वाले एक वृत्त की दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB = 90° है।
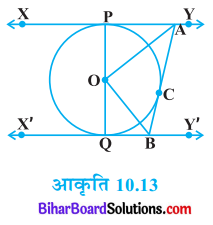
हल
दिया है : O केन्द्र वाले वृत्त की XY तथा X’Y’ दो समान्तर स्पर्श रेखाएँ हैं। वृत्त पर एक बिन्दु C से स्पर्श रेखा AB खींची गई है जो XY को A पर तथा X’Y’ को B पर काटती है। OA तथा OB को मिलाया गया है।
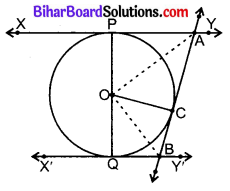
सिद्ध करना है : ∠AOB = 90°
रचना : रेखाखण्ड OC खींचा।
उपपत्ति : ∵ XY और X’Y’ वृत्त की दो समान्तर स्पर्श रेखाएँ हैं जो वृत्त को (माना) P तथा Q पर स्पर्श करती हैं। C से वृत्त की एक स्पर्श रेखा AB, XY को A पर तथा X’Y’ को B पर काटती है।
∴ बिन्दु A से वृत्त पर AP व AC स्पर्श रेखाएँ हैं।
तब, ∆OPA व ∆OCA में,
OP = OC (वृत्त की त्रिज्याएँ हैं)
AP = AC (बाह्य बिन्दु से वृत्त की स्पर्श रेखाएँ हैं)
OA = OA (उभयनिष्ठ भुजा है)
∆OPA ≅ ∆OCA
∠POA = ∠AOC …….(1)
इसी प्रकार, बिन्दु B से वृत्त पर BQ और BC स्पर्श रेखाएँ हैं।
तब, ∆OQB तथा ∆OBC में,
OQ = OC (वृत्त की त्रिज्याएँ हैं)
BQ = BC (बिन्दु B से वृत्त की स्पर्श रेखाएँ हैं)
OB = OB (उभयनिष्ठ भुजा है)
∆OQB ≅ ∆OBC
∠BOQ = ∠COB …….(2)
∵ ∠POA + ∠AOC + ∠COB + ∠BOQ = 180°
⇒ ∠AOC + ∠AOC + ∠COB + ∠COB = 180° [समीकरण (1) व समीकरण (2) से]
⇒ 2(∠AOC + ∠COB) = 180°
⇒ ∠AOC + ∠COB = 90°
अतः ∠AOB = 90°
इति सिद्धम्
![]()
प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल
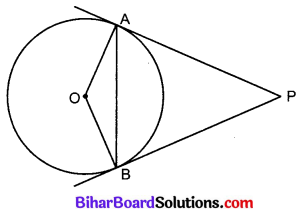
दिया है : O केन्द्र वाले वृत्त के बाहर एक बिन्दु P है। Pसे वृत्त पर PA तथा PB दो स्पर्श रेखाएँ खींची गई हैं। स्पर्श रेखाओं के बीच का ∠APB है। स्पर्श बिन्दुओं को रेखा AB मिलाती है जो वृत्त के केन्द्र पर ∠AOB बनाती है।
सिद्ध करना है : ∠APB, ∠AOB का सम्पूरक है।
उपपत्ति: ∵ OA वृत्त की त्रिज्या है और बाह्य बिन्दु P से PA स्पर्श रेखा है जो वृत्त को बिन्दु A पर स्पर्श करती है।
∴ ∠OAP = 90° …….(1)
इसी प्रकार, OB वृत्त की त्रिज्या है और बाह्य बिन्दु P से PB वृत्त की स्पर्श रेखा है जो वृत्त को बिन्दु B पर स्पर्श करती है।
∴ ∠OBP = 90° …….(2)
समीकरण (1) व (2) को जोड़ने पर,
∠OAP + ∠OBP = 180°
तब, चतुर्भुज OAPB में,
∠AOB + ∠OAP + ∠OBP + ∠APB = 360°
⇒ ∠AOB + 180° + ∠APB = 360°
⇒ ∠AOB + ∠APB = 360° – 180° = 180°
⇒ ∠AOB + ∠APB = 180°
अत: ∠APB, ∠AOB का सम्पूरक है।
इति सिद्धम्
प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज, समचतुर्भुज होता है।
हल
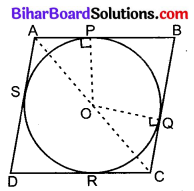
दिया है : केन्द्र O वाले वृत्त के परिगत खींचा गया समान्तर चतुर्भुज ABCD जिसकी भुजाएँ वृत्त को क्रमशः P, Q, R और S बिन्दुओं पर स्पर्श करती हैं।
सिद्ध करना है : ABCD एक समचतुर्भुज है।
रचना : AC, OP और OQ को मिलाया।
उपपत्ति : चूँकि बाह्य बिन्दु से वृत्त पर खींची गई दोनों स्पर्श रेखाएँ लम्बाई में बराबर होती हैं,
∴ AP = AS, BP = BQ, CQ = CR तथा DR = DS
अब, ∆OAP और ∆OCQ में,
OP = OQ (एक ही वृत्त की त्रिज्याएँ हैं)
∠OAP = ∠OCQ (समान्तर चतुर्भुज के सम्मुख कोणों के अर्द्धक हैं)
∠OPA = ∠OQC (प्रत्येक समकोण है)
दोनों त्रिभुज सर्वांगसम हैं अर्थात् ∆OAP ≅ ∆OCQ
⇒ AP = CQ
⇒ AP + BP = CQ + BQ (∵ BP = BQ)
⇒ AB = BC
इसी प्रकार सिद्ध कर सकते हैं कि AD = AB तथा BC = CD
∴ समान्तर चतुर्भुज ABCD में,
AB = CD = BC = AD
अत: ABCD एक समचतुर्भुज है।
इति सिद्धम्
![]()
प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु Dद्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 cm और 6 cm हैं। भुजाएँ AB और AC ज्ञात कीजिए।
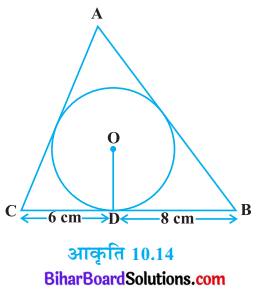
हल
चित्र में, ABC एक त्रिभुज है जिसके अन्तर्वृत्त का केन्द्र O है तथा अन्तर्वृत्त की त्रिज्याएँ OD = OE = OF = 4 cm हैं।
स्पर्श बिन्दु D से BC के खण्ड BD = 6 cm तथा DC = 8 cm हैं।
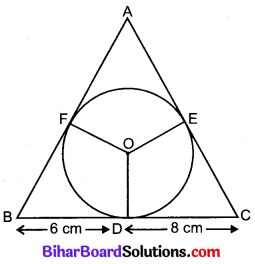
तब, BF = 6 cm तथा CE = 8 cm
माना AF = AE = x cm
तब, AB = AF + BF = (x + 6) cm
⇒ c = (x + 6) cm [∵ ∆ABC से BC = a, AB = c, CA = b]
BC = 8 + 6 = 14 cm
⇒ a = 14 cm
तथा CA = AE + CE = (x + 8) cm
⇒ b = (x + 8) cm
∵ s = \(\frac{a+b+c}{2}\)
s = \(\frac{14+(x+8)+(x+6)}{2}=\frac{2 x+28}{2}\) = (x + 14)
(s – a) = (x + 14) – 14 = x
(s – b) = (x + 14) – (x + 8) = 6
(s – c) = (x + 14) – (x + 6) = 8

दोनों पक्षों का वर्ग करने पर,
3x2 + 42x = (x + 14)2
⇒ 3x2 + 42x = x2 + 28x + 196
⇒ 3x2 + 42x – x2 – 28x – 196 = 0
⇒ 2x2 + 14x – 196 = 0
⇒ x2 + 7x – 98 = 0
⇒ x2 + (14 – 7)x – 98 = 0
⇒ x2 + 14x – 7x – 98 = 0
⇒ (x2 + 14x) – (7x + 98) = 0
⇒ x(x + 14) – 7(x + 14) = 0
⇒ (x + 14) (x – 7) = 0
यदि x + 14 = 0, तो x = -14
और यदि x – 7 = 0, तो x = 7
x का मान -14 ऋणात्मक है जो लम्बाई नहीं हो सकता। अत: यह स्वीकार्य नहीं है।
तब, x = 7
∴ भुजा AB = x + 6 = 7 + 6 = 13 cm
तथा भुजा CA = x + 8 = 7 + 8 = 15 cm
अत: त्रिभुज की अन्य दो भुजाएँ AB व CA क्रमश: 13 cm व 15 cm हैं।
![]()
प्रश्न 13.
सिद्धं कीजिए कि वृत्त के परिगत बने चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल
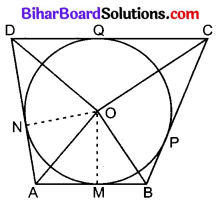
दिया है : केन्द्र O वाले वृत्त के परिगत चतुर्भुज ABCD खींचा गया है जिसकी भुजाएँ AB, BC, CD व DA वृत्त को क्रमशः बिन्दुओं M, P, Q व N पर स्पर्श करती हैं।
सिद्ध करना है : ∠AOB + ∠COD = 180°
रचना : स्पर्श बिन्दु M और N को केन्द्र O से मिलाया।
उपपत्ति : माना ∠A = 2α, ∠B = 2β, ∠C = 2γ, ∠D = 2δ
∆OAM और ∆OAN में,
∠OMA = ∠ONA (प्रत्येक समकोण है)
OM = ON (एक ही वृत्त की त्रिज्या है)
OA = OA
∴ दोनों त्रिभुज सर्वांगसम हैं अर्थात् ∆OAM ≅ ∆OAN
⇒ ∠OAM = ∠OAN = \(\frac{1}{2}\) (∠A) = \(\frac{1}{2}\) (2α) = α
⇒ ∠OAB = ∠OAD = α
इसी प्रकार, ∠OBA = ∠OBC = β
∠OCB = ∠OCD = γ
तथा ∠ODA = ∠ODC = δ
अब, ∆AOB में,
∠AOB = 180° – ∠OAB – ∠OBA = 180° – α – β = 180° – (α + β)
तथा ∠COD = 180° – ∠OCD – ∠ODC = 180° – γ – δ = 180° – (γ + δ)
समीकरण (1) व (2) को जोड़ने पर,
∠AOB + ∠COD = {180° – (α + β)} + {180° – (γ + δ)}
⇒ ∠AOB + ∠COD = 360° – (α + β + γ + δ)
परन्तु ∠A + ∠B + ∠C + ∠D = 360°
⇒ 2α + 2β + 2γ + 2δ = 360°
⇒ α + β + γ + δ = 180°
अत: समीकरण (3) से,
∠AOB + ∠COD = 360° – 180° = 180°
इति सिद्धम्