Bihar Board Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.2 Text Book Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 11 रचनाएँ Ex 11.2
Bihar Board Class 10 Maths रचनाएँ Ex 11.2
निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए-
प्रश्न 1.
6 cm त्रिज्या का एक वृत्त खींचिए। केन्द्र से 10 cm दूर एक बिन्दु से वृत्त पर स्पर्श रेखा-युग्म की रचना कीजिए और उनकी लम्बाइयाँ मापकर लिखिए।
हल
दिया है : 6 cm त्रिज्या का एक वृत्त और उसके केन्द्र O से 10 cm दूरी पर एक बिन्दु P.
रचना करनी है : वृत्त के स्पर्श रेखा-युग्म की।
रचना विधि :
1. सर्वप्रथम बिन्दु O को केन्द्र मानकर 6 cm त्रिज्या का एक वृत्त खींचा।
2. वृत्त के केन्द्र O से 10 cm की दूरी पर एक बिन्दु P लिया।
3. OP को मिलाया।
4. OP को व्यास मानकर एक वृत्त खींचा जिसने केन्द्र O वाले वृत्त को T1 और T2 बिन्दुओं पर काटा।
5. PT1 और PT2 को मिलाया जो वृत्त की अभीष्ट स्पर्श रेखाएँ हैं।
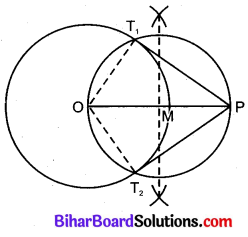
मापने पर : PT1 = PT2 = 8.0 cm
उपपत्ति : रेखाखण्ड OT1 व OT2 खींचिए।
∵ OP व्यास है।
∴ OT1P तथा OT2P अर्द्धवृत्त हैं
∵ ∠OT1P, अर्द्धवृत्त OT1P में तथा ∠OT2P, अर्द्धवृत्त ∠OT2P में स्थित हैं।
∠OT1P = 90° तथा ∠OT2P = 90°
∵ OT1 और OT2, केन्द्र O वाले वृत्त की त्रिज्याएँ हैं जिनके सिरों T1 व T2 पर T1P तथा T2P समकोण बनाती हैं।
अत: PT1 तथा PT2 स्पर्श रेखाएँ हैं।
इति सिद्धम्
![]()
प्रश्न 2.
4 cm त्रिज्या के एक वृत्त पर 6 cm त्रिज्या के एक संकेन्द्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लम्बाई मापिए। परिकलन से इस माप की जाँच भी कीजिए।
हल
दिया है : 4 cm त्रिज्या का एक वृत्त और 6 cm त्रिज्या का एक संकेन्द्रीय वृत्त जिस पर एक बिन्दु P है।
रचना करनी है : 4 cm त्रिज्या वाले वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. 4 cm त्रिज्या लेकर केन्द्र O वाला एक वृत्त खींचा।
2. केन्द्र O से 6 cm त्रिज्या का एक संकेन्द्रीय वृत्त खींचा और इस पर एक बिन्दु लिया।
3. रेखाखण्ड OP खींचा और इसका लम्ब समद्विभाजक खींचा जो OP को बिन्दु M पर काटता है।
4. केन्द्र M से OP व्यास का एक वृत्त खींचा जो केन्द्र O के 4 cm त्रिज्या वाले वृत्त को T1 तथा T2 पर काटता है।
5. रेखाखण्ड PT1 तथा PT2 खींचा।
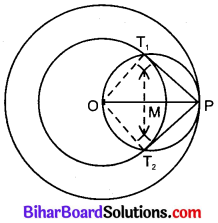
PT1 तथा PT2 अभीष्ट स्पर्श रेखाएँ हैं।
मापने पर : PT1 = 4.5 cm तथा PT2 = 4.5 cm
परिकलन :

औचित्य : ∠OT1P = ∠OT2P = 90°
∵ दोनों कोण OP व्यास वाले वृत्त के अन्दर अर्द्धवृत्त के कोण हैं।
∴ OT1 ⊥ PT1, OT2 ⊥ PT2
अत: रेखाएँ PT1 व PT2 अभीष्ट स्पर्शियाँ हैं।
इति सिद्धम्
![]()
प्रश्न 3.
3 cm त्रिज्या का एक वृत्त खींचिए। इसके किसी बढ़ाए गए व्यास पर केन्द्र से 7 cm की दूरी पर स्थित दो बिन्दु P और Q लीजिए। इन दोनों बिन्दुओं से वृत्त पर स्पर्श रेखाएँ खींचिए।
हल
दिया है : एक वृत्त जिसका केन्द्र 0 है तथा त्रिज्या 3 cm है। AOB वृत्त का एक व्यास है जिसको इस प्रकार बिन्दुओं P व Q तक बढ़ाया गया है कि वृत्त के केन्द्र O से प्रत्येक बिन्दु P व Q की दूरियाँ OP व OQ = 7 cm हैं।
रचना करनी है : बिन्दुओं P व Q से वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. O केन्द्र वाला 3 cm त्रिज्या का एक वृत्त खींचा।
2. इसका व्यास AOB खींचा और इसे दोनों ओर क्रमश: P व Q तक इस प्रकार बढ़ाया कि OP = OQ = 7 cm
3. OP व OQ के मध्य बिन्दु क्रमश: M1 व M2 ज्ञात किए।
4. केन्द्र M1 से M1O त्रिज्या का एक वृत्त खींचा जो O केन्द्र वाले वृत्त को बिन्दुओं T1 व T2 पर काटता है।
5. रेखाखण्ड PT1 व PT2 खींचे।
6. केन्द्र M2 से M2O त्रिज्या का एक वृत्त खींचा जो O केन्द्र वाले वृत्त को बिन्दुओं S1 व S2 पर काटता है।
7. रेखाखण्ड QS1 तथा QS2 खींचे।
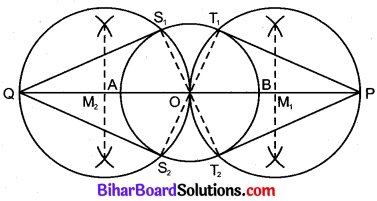
रेखाखण्ड PT1, PT2, QS1 व QS2 अभीष्ट स्पर्श रेखाएँ हैं।
उपपत्ति : केन्द्र O वाले वृत्त की त्रिज्याएँ OT1, OT2, OS1 व OS2 खींची।
∵ केन्द्र M वाले वृत्त में ∠OT1P व ∠OT2P अर्द्धवृत्तों में स्थित कोण हैं।
∴ ∠OT1P व ∠OT2P समकोण हैं जो क्रमशः त्रिज्याओं OT1 व OT2 के सिरों T1 व T2 पर स्थित हैं।
∴ PT1 व PT2 केन्द्र O वाले वृत्त की स्पर्श रेखाएँ हैं।
इसी प्रकार, QS1 व QS2 भी केन्द्र O वाले वृत्त की स्पर्शरेखाएँ हैं।
इति सिद्धम्
![]()
प्रश्न 4.
5 cm त्रिज्या के एक वृत्त पर ऐसी दो स्पर्श रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झकी हों।
हल
दिया है : एक वृत्त जिसका केन्द्र O है तथा त्रिज्या 5 cm है।
रचना करनी है : वृत्त की दो स्पर्श रेखाओं की जिनके बीच का कोण 60° हो।
विश्लेषण : माना वृत्त का केन्द्र O तथा PT और BT इसकी दो स्पर्श रेखाएँ हैं जिनके बीच का कोण 60° है।
∵ ∠PTB = 60°
∴ ∠POB = 180° – 60° = 120°
⇒ ∠POA = 60°
रचना विधि :
1. बिन्दु O को केन्द्र मानकर 5 cm त्रिज्या का एक वृत्त खींचा।
2. वृत्त का एक व्यास AB खींचा।
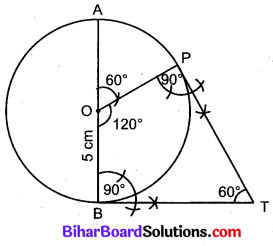
3. बिन्दु O पर OA से 60° का कोण बनाती हुई एक रेखा OP खींची जो वृत्त को बिन्दु P पर काटती है।
4. बिन्दु B पर OB के लम्बवत् एक रेखा खींची तथा बिन्दु P पर OP के लम्बवत् एक रेखा खींची। दोनों रेखाएँ एक-दूसरे को बिन्दु T पर काटती हैं।
अत: PT और BT वृत्त की दो अभीष्ट स्पर्श रेखाएँ हैं जो एक-दूसरे के साथ 60° का कोण बनाती हैं।
औचित्य : उपर्युक्त विश्लेषण ही अभीष्ट औचित्य है।
![]()
प्रश्न 5.
8 cm लम्बा एक रेखाखण्ड AB खींचिए। A को केन्द्र मानकर 4 cm त्रिज्या का एक वृत्त तथा B को केन्द्र मानकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखाओं की रचना कीजिए।
हल
दिया है : रेखाखण्ड AB = 8.0 cm। केन्द्र A से 4 cm त्रिज्या का एक वृत्त खींचा गया है तथा केन्द्र B से 3 cm त्रिज्या का एक अन्य वृत्त खींचा गया है।
रचना करनी है : केन्द्र बिन्दु A से केन्द्र B वाले वृत्त की दो स्पर्श रेखाओं तथा बिन्दु B से केन्द्र A वाले वृत्त की दो स्पर्श रेखाओं की।
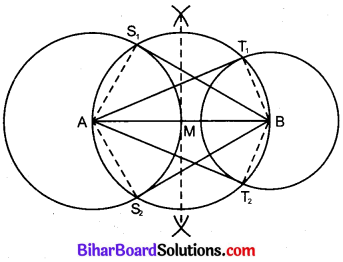
रचना विधि:
1. रेखाखण्ड AB= 8 cm खींचा।
2. केन्द्र A से 4 cm त्रिज्या का एक वृत्त खींचा और केन्द्र B से 3 cm त्रिज्या का एक वृत्त खींचा।
3. AB का मध्य बिन्दु M ज्ञात किया।
4. M को केन्द्र मानकर AB व्यास का एक वृत्त खींचा जो A केन्द्र वाले वृत्त को बिन्दुओं S1 व S2 पर तथा B केन्द्र वाले वृत्त को बिन्दुओं T1 व T2 पर काटता है।
5. रेखाखण्ड S1B व S2B तथा AT1 व AT2 खींचे।
S1B व S2B केन्द्र A वाले वृत्त की तथा AT1 व AT2 केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।
उपपत्ति : ∵ केन्द्र M वाले वृत्त का AB व्यास है।
∴ ∠AS1B, ∠AS2B, ∠AT1B व ∠AT2B अर्द्धवृत्त के कोण हैं। अत: प्रत्येक समकोण है।
रेखाखण्ड AS1 व AS2 केन्द्र A वाले वृत्त और BT1 व BT2 केन्द्र B वाले वृत्त की त्रिज्याएँ हैं।
∴ S1B व S2B केन्द्र A वाले वृत्त और AT1 व AT2 केन्द्र B वाले वृत्त की स्पर्श रेखाएँ हैं।
इति सिद्धम्
![]()
प्रश्न 6.
ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC = 8 cm तथा ∠B = 90° है। B से AC पर BD लम्ब है। बिन्दुओं B, C व D से होकर जाने वाला एक वृत्त खींचा गया है। A से इस वृत्त पर स्पर्श रेखा की रचना कीजिए।
हल
दिया है : एक समकोण त्रिभुज ABC में AB = 6 cm, BC = 8 cm तथा ∠B = 90°| B से भुजा AC पर BD लम्ब खींचा गया है।
रचना करनी है : एक ऐसे वृत्त की जो बिन्दुओं B, C तथा D से होकर जाता है और बिन्दु A से इस वृत्त की स्पर्श रेखा की।
रचना विधि :
1. सर्वप्रथम दिए गए समकोण त्रिभुज ABC की रचना की।
2. बिन्दु B से AC पर लम्ब खींचा जो AC को D पर मिलता है।
3. ∆BCD की भुजाओं BD तथा CD के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दुओं O पर काटते हैं।
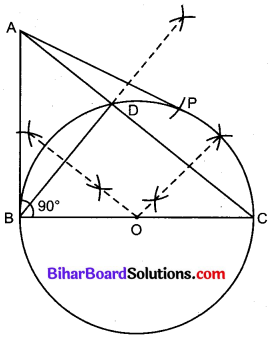
4. O को केन्द्र मानकर OB त्रिज्या से एक वृत्त खींचा जो बिन्दुओं B, C व D से होकर जाएगा।
5. AB स्वयं स्पर्श रेखा है; अत: A को केन्द्र BP मानकर AB त्रिज्या से चाप खींचे जो वृत्त को बिन्दु P पर काटते हैं।
AP अभीष्ट स्पर्श रेखा है।
औचित्य : ∠ABC = 90°, अत: रेखा AB स्वयं स्पर्श रेखा है।
AP = AB अतः रेखा AB, बिन्दु A से खींची गई दूसरी स्पर्श-रेखा है।
इति सिद्धम्
![]()
प्रश्न 7.
किसी चूड़ी की सहायता से एक वृत्त खींचिए। वृत्त के बाहर एक बिन्दु लीजिए। इस बिन्दु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए।
हल
दिया है : एक वृत्त जिसका केन्द्र ज्ञात नहीं है। वृत्त के बाहर एक बिन्दु P है।
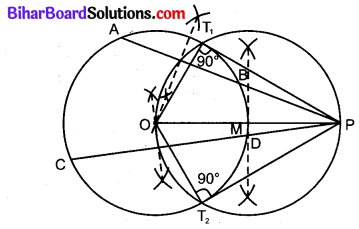
रचना करनी है : बिन्दु P से वृत्त की स्पर्श रेखाओं की।
रचना विधि :
1. बिन्दु P से ABP तथा CDP दो छेदक रेखाएँ खींची।
2. जीवाओं AB व CD के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दु O पर काटते हैं। बिन्दु O दिए गए वृत्त का केन्द्र होगा।
3. रेखाखण्ड OP खींचा और इसका मध्य बिन्दु M ज्ञात किया।
4. M को केन्द्र मानकर MO त्रिज्या (OP व्यास) का वृत्त खींचा जो दिए गए वृत्त को क्रमश: बिन्दुओं T1 व T2 पर काटता है।
5. रेखाखण्ड PT1 व PT2 खींचे।
रेखाखण्ड PT1 व PT2 अभीष्ट स्पर्श रेखाएँ हैं।
औचित्य : केन्द्र O के बिन्दुओं T1 व T2 से मिलाया।
∠OT1P = ∠OT2P = 90° (अर्द्धवृत्त के कोण हैं)
∴ रेखाएँ PT1 व PT2 अभीष्ट स्पर्शियाँ हैं।
इति सिद्धम्