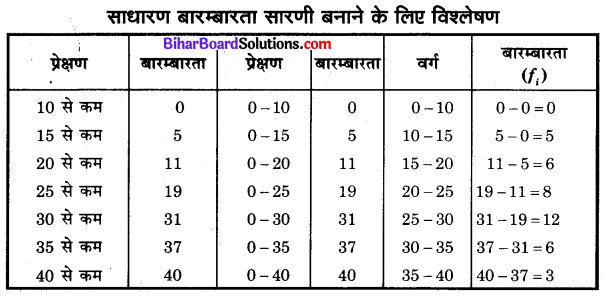
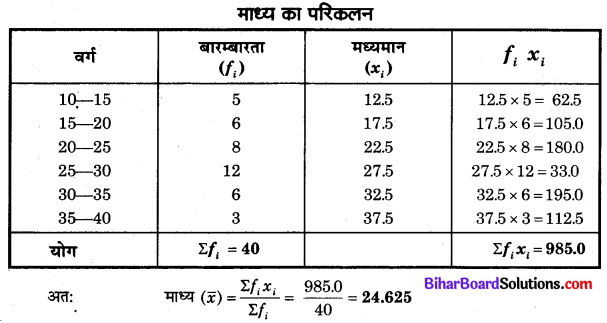
Bihar Board Class 10 Maths Solutions Chapter 14 सांख्यिकी Additional Questions and Answers.
BSEB Bihar Board Class 10 Maths Solutions Chapter 14 सांख्यिकी Additional Questions
Bihar Board Class 10 Maths सांख्यिकी Additional Questions
बहुविकल्पीय प्रश्न
प्रश्न 1.
सूत्र \(\bar{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\) में, वर्गीकृत आँकड़ों का माध्य ज्ञात करने के लिए a से विचलन
di है, a है
(i) वर्गों की निम्न सीमाएँ
(ii) वर्गों की उच्च सीमाएँ
(iii) वर्गों के मध्य-बिन्दु
(iv) वर्गों की बारम्बारताएँ
हल
(iii) वर्गों के मध्य-बिन्दु
प्रश्न 2.
जब वर्गीकृत आँकड़ों के माध्य की गणना करते हैं, तो हम मानते हैं कि बारम्बारताएँ हैं
(i) सभी वर्गों के लिए समान बंटित
(ii) वर्गों के वर्ग अंक पर केन्द्रित
(iii) वर्गों की उच्च सीमा पर केन्द्रित
(iv) वर्गों की निम्न सीमा पर केन्द्रित
हल
(ii) वर्गों के वर्ग अंक पर केन्द्रित
![]()
प्रश्न 3.
यदि xi वर्गीकृत आँकड़ों के वर्ग अन्तरालों के मध्य बिन्दु तथा fi उनकी संगत बारम्बारताएँ और \(\bar{x}\) माध्य हो, तो \(\Sigma\left(f_{i} x_{i}-\bar{x}\right)\) बराबर है
(i) 0
(ii) -1
(iii) 1
(iv) 2
हल
(i) 0
प्रश्न 4.
सूत्र \(\bar{x}=a+h \frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\) में, वर्गीकृत बारम्बारता बंटन का माध्य ज्ञात करने के लिए ui बराबर है
(i) \(\frac{x_{i}+a}{h}\)
(ii) h(xi – a)
(iii) \(\frac{x_{i}-a}{h}\)
(iv) \(\frac{a-x_{i}}{h}\)
हल
(iii) \(\frac{x_{i}-a}{h}\)
![]()
प्रश्न 5.
वर्गीकृत आँकड़ों का ‘से कम प्रकार का’ और ‘से अधिक प्रकार का’ संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के भुज (x-अक्ष) पर काटता है, तब इससे प्राप्त होता है
(i) माध्य
(ii) माध्यिका
(iii) बहुलक
(iv) ये सभी
हल
(ii) माध्यिका
प्रश्न 6.
निम्नलिखित बंटन के लिए

बहुलक वर्ग और माध्यिका वर्ग की निम्न सीमाओं का योग है
(i) 15
(ii) 25
(iii) 30
(iv) 35
हल
(ii) 25
![]()
प्रश्न 7.
निम्नलिखित बारम्बारता बंटन के लिए

माध्यिका वर्ग की उच्च सीमा है।
(i) 17
(ii) 17.5
(iii) 18
(iv) 18.5
हल
(iii) 18
प्रश्न 8.
निम्नलिखित बंटन के लिए
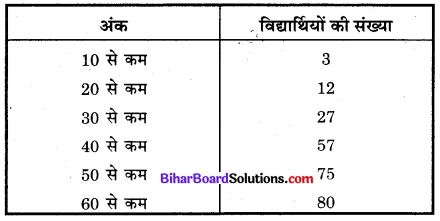
बहुलक वर्ग है
(i) 10 – 20
(ii) 20 – 30
(iii) 30 – 40
(iv) 50 – 60
हल
(iii) 30 – 40
![]()
प्रश्न 9.
दिए आँकड़े हैं

माध्यिका वर्ग की उच्च सीमा और बहुलक वर्ग की निम्न सीमा का अन्तर है।
(i) 0
(ii) 19
(iii) 20
(iv) 38
हल
(iii) 20
प्रश्न 10.
110 मी की बाधा दौड़ में 150 एथलीटों द्वारा लिया गया समय (सेकंड में) नीचे सारणीबद्ध किया गया है।

एथलीटों की संख्या जिन्होंने रेस को 14.6 सेकण्ड से कम समय में पूरा किया है।
(i) 11
(ii) 71
(iii) 82
(iv) 130
हल
(iii) 82
![]()
प्रश्न 11.
निम्नलिखित बंटन में विद्यार्थियों की संख्या
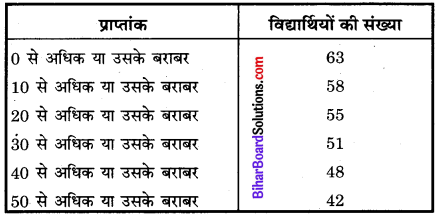
वर्ग 30 – 40 की बारम्बारता है
(i) 3
(ii) 4
(iii) 48
(iv) 51
हल
(i) 3
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
गणित विषय की परीक्षा में 10 छात्रों ने निम्नलिखित अंक प्राप्त किये
38, 17, 20, 8, 19, 35, 45, 15, 34, 14
प्राप्तांकों की माध्यिका ज्ञात कीजिए।
हल
पदों को आरोही क्रम में रखने पर,
8, 14, 15, 17, 19, 20, 34, 35, 38, 45
पदों की संख्या N = 10 है जो कि सम है।

प्रश्न 2.
किसी बंटन का माध्य ज्ञात कीजिए यदि इसकी माध्यिका 45 और बहुलक 13 हो।
हल
बहुलक, माध्य तथा माध्यिका के बीच सम्बन्ध :
बहुलक = 3 × माध्यिका – 2 × माध्य
अथवा 2 × माध्य = 3 × माध्यिका – बहुलक
= 3 × 45 – 13
= 135 – 13
= 122
माध्य = \(\frac{122}{2}\) = 61
![]()
प्रश्न 3.
यदि किसी बंटन का माध्य 16 और बहुलक 13 हो तो बंटन माध्यिका ज्ञात कीजिए।
हल
बहुलक = 3 × माध्यिका – 2 × माध्य
⇒ 13 = 3(माध्यिका) – 2 × 16
⇒ 3(माध्यिका) = 13 + 32 = 45
⇒ माध्यिका = \(\frac{45}{3}\) = 15
प्रश्न 4.
यदि प्रेक्षणों x1, x2, x3, ….., xn, की बारम्बारताएँ क्रमशः f1, f2, f3,…..,fn हों तो इनका माध्य ज्ञात करने के लिए सूत्र लिखिए।
हल

प्रश्न 5.
निम्न आँकड़ों का बहुलक ज्ञात कीजिए :
6, 9, 8, 7, 6, 7, 3, 6, 5, 6, 4
हल
उक्त आँकड़ों के निरीक्षण से हमें ज्ञात होता है कि आँकड़े 6 की आवृत्ति अधिकतम है।
अत: बहुलक = 6
![]()
प्रश्न 6.
बहुलक को परिभाषित कीजिए।
हल
आँकड़ों के किसी संग्रह या संकलन में जिस प्रेक्षण की आवृत्ति (बारम्बारता) अधिकतम होती है। उस प्रेक्षण को संग्रह का ‘बहुलक’ कहते हैं।
लघु उत्तरीय प्रश्न
प्रश्न 1.
निम्नलिखित आँकड़ों से माध्य ज्ञात कीजिए

हल
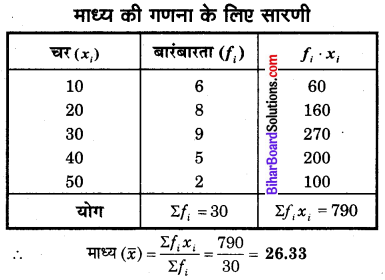
प्रश्न 2.
एक कक्षा के 50 छात्रों के भार नीचे की सारणी में प्रदर्शित हैं

इन छात्रों के भार का माध्य ज्ञात कीजिए।
हल
माना कल्पित माध्य, A = 47 किग्रा
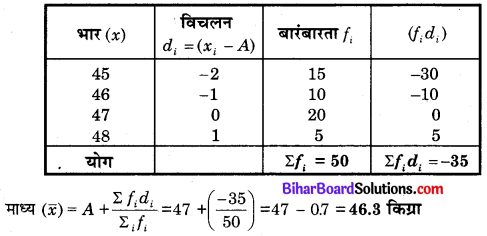
प्रश्न 3.
निम्नलिखित आँकड़ों का माध्य ज्ञात कीजिए

हल
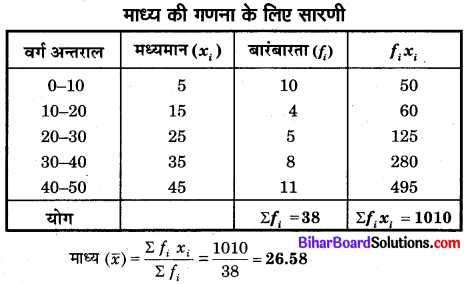
प्रश्न 4.
निम्नलिखित सारणी से माध्य की गणना कीजिए

हल
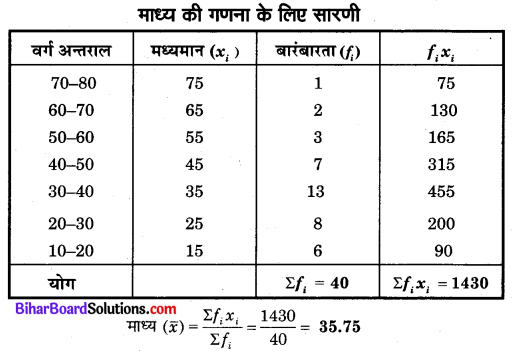
प्रश्न 5.
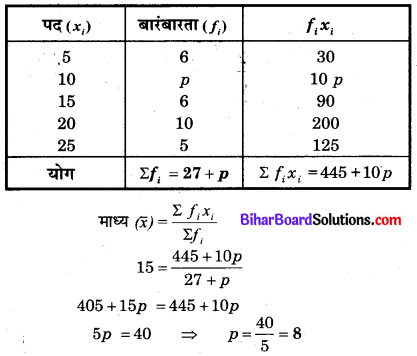
यदि निम्नांकित आँकड़ों का माध्य 15 है तो p का मान ज्ञात कीजिए
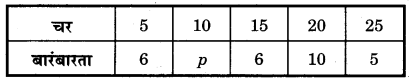
हल
प्रश्न 6.
यदि निम्नलिखित बारम्बारता बंटन का माध्य 1.46 है, तो f1 और f2 के मान ज्ञात कीजिए:

बारंबारताओं का कुल योगफल 200 है।
हल
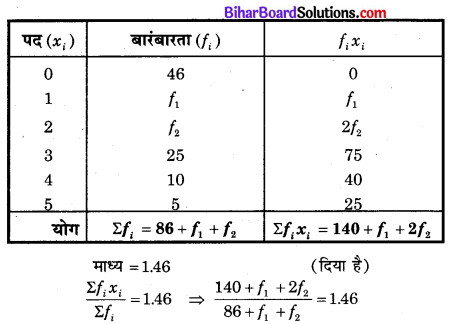
⇒ 140 + f1 + 2f2 = 1.46 (86 + f1 + f2) …….(1)
पुनः बारंबारताओं का योग 86 + f1 + f2 = 200
⇒ f1 + f2 = 114 …….(2)
समी० (2) से (f1 + f2) का मान समी० (1) में रखने पर,
140 + f1 + 114 = 1.46(86 + 114)
⇒ f1 = 292 – 254 = 38
समी० (2) से f2 + 38 = 114
⇒ f2 = 76
अत: f1 और f2 के मान क्रमशः 76 व 38 हैं।
![]()
प्रश्न 7.
निम्नलिखित बारंबारता बंटन की माध्यिका ज्ञात कीजिए

हल
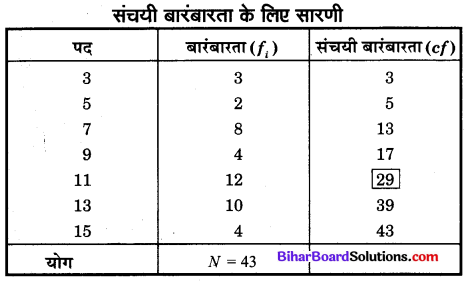
यहाँ, N = 43 अर्थात् पदों की संख्या विषम है।
मध्य पद = \(\left(\frac{N+1}{2}\right)\) वाँ पद
= \(\frac{43+1}{2}\) वाँ पद
= 22 वाँ पद
संचयी बारंबारता सारणी से स्पष्ट है कि 22वाँ पद उस समूह में है जिसकी संचयी बारंबारता 29 है।
माध्यिका = 22वें पद का मान = 11
प्रश्न 8.
निम्नलिखित सारणी में माध्यिका जेब खर्च ज्ञात कीजिए

हल
आँकड़ों को आरोही क्रम में रखते हुए संचयी बारंबारता सारणी बनाने पर
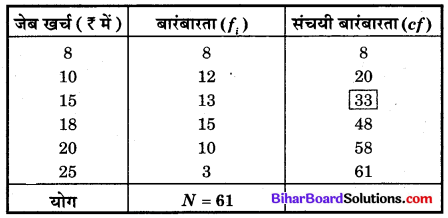
यहाँ, N = 61 अर्थात् पदों की संख्या विषम है।
मध्य पद = \(\left(\frac{N+1}{2}\right)\) वाँ पद
= \(\frac{61+1}{2}\) वाँ पद
= 31 वाँ पद
संचयी बारंबारता सारणी से स्पष्ट है कि 31वाँ पद उस समूह में है जिसकी संचयी बारंबारता 33 है।
माध्यिका = 33 वें पद का मान = 15
![]()
प्रश्न 9.
निम्नलिखित सारणी से माध्यिका और बहुलक ज्ञात कीजिए
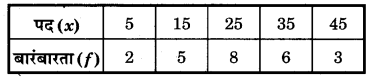
हल
संचयी बारंबारता के लिए सारणी
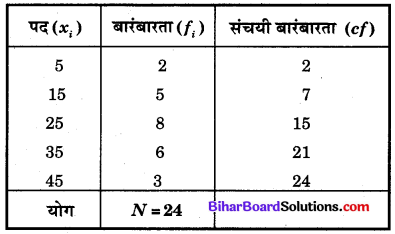
यहाँ n = 24 अर्थात् पदों की संख्या सम है।
मध्य पद = \(\frac{N}{2}\) वाँ पद + (\(\frac{N}{2}\) + 1) वाँ पद
= \(\frac{24}{2}+\left(\frac{24}{2}+1\right)\) वाँ पद अर्थात् 12वाँ व 13वाँ पद
संचयी बारंबारता सारणी से स्पष्ट है कि 12वाँ व 13वाँ पद उस समूह में है जिसकी संचयी बारंबारता 15 है।
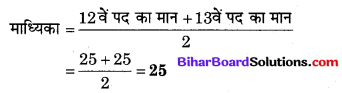
पुनः चूँकि सर्वाधिक बारंबारता 8 पद 25 की है।
अभीष्ट बहुलक = 25
प्रश्न 10.
निम्नलिखित आँकड़ों का बहुलक ज्ञात कीजिए।

हल
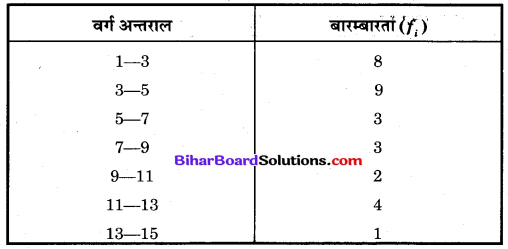
बहुलक के लिए वर्ग 3 – 5 है।
बहुलक वर्ग की निम्न सीमा (l1) = 3
बहुलक वर्ग की उच्च सीमा (l2) = 5
बहुलक वर्ग का विस्तार (h) = l2 – l1 = 5 – 3 = 2
बहुलक वर्ग की बारम्बारता (f) = 9
बहुलक वर्ग से ठीक पूर्व की बारम्बारता (f1) = 8
बहुलक वर्ग से ठीक बाद की बारम्बारता (f2) = 3

![]()
प्रश्न 11.
निम्नलिखित बारम्बारता बंटन सारणी को ध्यान से पढ़िए तथा b और d के मान लिखिए
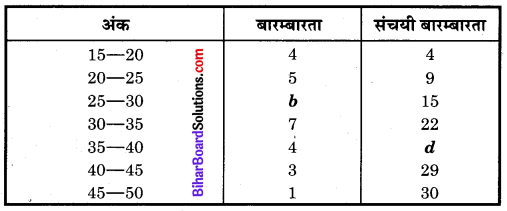
हल
वर्ग 25 – 30 की संचयी बारम्बारता = 9 + b
प्रश्नानुसार, संचयी बारम्बारता = 15
⇒ 9 + b = 15
⇒ b = 15 – 9 = 6
इसी प्रकार, वर्ग 35 – 40 की संचयी बारम्बारता = 22 + 4 = 26
प्रश्नानुसार, संचयी बारम्बारता = d
⇒ d = 26
अतः b = 6 और d = 26
प्रश्न 12.
कक्षा X के 100 विद्यार्थियों द्वारा गणित में प्राप्त अंक नीचे सारणी में दिए गए हैं। प्राप्त अंकों का माध्यक ज्ञात कीजिए।

हल
असतत श्रेणी को सतत श्रेणी में बदलने पर,
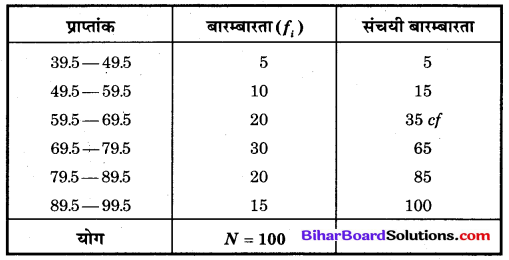
यहाँ, N = 100
⇒ \(\frac{N}{2}=\frac{100}{2}=50\)
संचयी बारम्बारता से स्पष्ट है कि 50 संचयी बारम्बारता 65 के अन्तर्गत है, इसलिए (69.5 – 79.5) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l1) = 69.5
माध्यिका वर्ग की उच्च सीमा (l2) = 79.5
माध्यिका वर्ग का वर्ग अन्तराल (h) = l2 – l1 = 79.5 – 69.5 = 10
माध्यिका वर्ग की बारम्बारता (f) = 30
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 35

दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
निम्नलिखित बारंबारता बंटन का माध्य लघु विधि (विचलन विधि) से ज्ञात कीजिए

हल
माना कल्पित माध्य, A = 35 है।
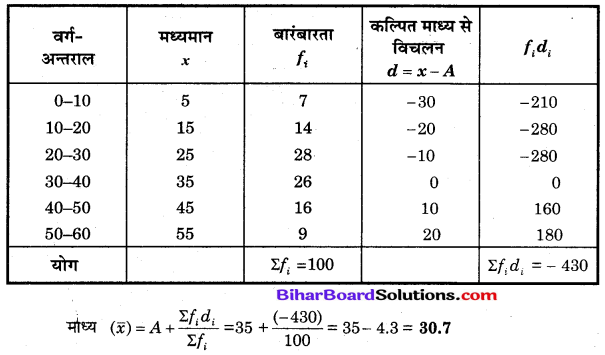
![]()
प्रश्न 2.
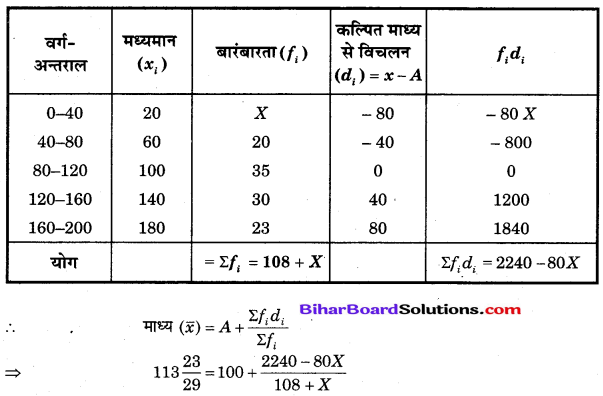
निम्नलिखित बारंबारता वितरण का माध्य 113\(\frac{23}{29}\) है। इसमें अज्ञात राशि X का मूल्य ज्ञात कीजिए।

हल
माना कल्पित माध्य, A = 100 है।

प्रश्न 3.
निम्नलिखित बंटनों की माध्यिका ज्ञात कीजिए

हल
उपर्युक्त बंटन की संचयी बारंबारता सारणी निम्नवत् है
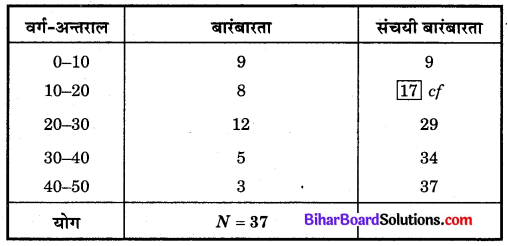
यहाँ N = 37
⇒ \(\frac{N}{2}=\frac{37}{2}=18.5\)
संचयी बारम्बारता सारणी से स्पष्ट है कि 18.5 संचयी बारम्बारता 29 के अन्तर्गत है, इसलिए (20 – 30) माध्यिका वर्ग हुआ।
माध्यिका वर्ग की निम्न सीमा (l1) = 20
माध्यिका वर्ग की उच्च सीमा (l2) = 30
माध्यिका वर्ग का वर्ग अन्तराल (h) = l2 – l1 = 30 – 20 = 10
माध्यिका वर्ग की बारम्बारता (f) = 12
माध्यिका वर्ग के ठीक पहले वर्ग की संचयी बारम्बारता (cf) = 17

![]()
प्रश्न 4.
निम्नलिखित बारम्बारता बंटन के लिए माध्य ज्ञात कीजिए :
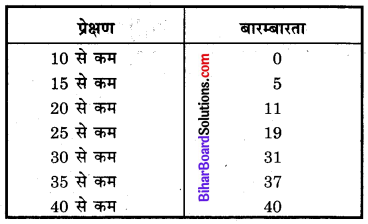
हल