Bihar Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.2 Textbook Questions and Answers.
BSEB Bihar Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.2
![]()
Question 1.
In figures, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
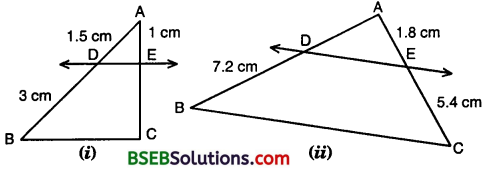
Solution:
(i) In Fig. (i),
since DE || BC, therefore
\(\frac { AD }{ DB }\) = \(\frac { AE }{ EC }\) or \(\frac { 1.5 }{ 3 }\) = \(\frac { 1}{ EC }\)
or EC = \(\frac { 3}{ 1.5}\) = \(\frac{3 \times 10}{15}\) Cm = 2 cm
(ii) In Fig. (ii),
since DE || BC, therefore
\(\frac { AD }{ DB }\) =\(\frac { AE }{ EC}\) or \(\frac { AD }{7.2 }\) = \(\frac { 1.8 }{ 5.4 }\)
or AD = \(\frac { 18 }{ 54 }\) x \(\frac { 72 }{ 10 }\) cm = 2.4 cm.
Question 2.
E and F are points on the sides PQ and PR respectively of a A PQR. For each of the following cases, state whether EF || QR :
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:
(i) We have :
PE = 3.9 cm, EQ = 3 cm,
PF = 3.6 cm and FR = 2.4 cm
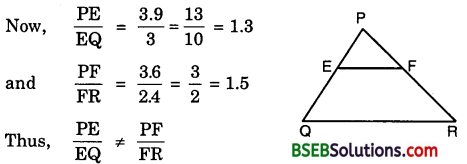
i. e., EF does not divide the sides PQ and PR of A PQR in the same ratio. Therefore, EF is not parallel to QR.
(ii) We have : PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Now, \(\frac { PE }{ EQ }\) = \(\frac { 4 }{ 4.5 }\) = \(\frac { 40 }{ 45 }\) = \(\frac { 8 }{ 9 }\)
and \(\frac { PF }{ FR }\) = \(\frac { 8 }{ 9 }\)
So, \(\frac { PE }{ EQ }\) = \(\frac { PF }{ FR }\)
Thus, EF divides sides PQ and PR of ∆ PQR in the same ratio. Therefore, by the converse of Basic Proportionality Theorem, we have EF || QR.
(iii) We have :PQ= 1.28 cm, PR = 2.56 cm,
PE = 0.18 cm and PF 0.36 cm
∴ EQ = PQ – PE = (1.28 – 0.18) cm = 1.10 cm
and FR = PR – PF = (2.56 – 0.36) = 2.20 cm
Now, \(\frac { PE }{ EQ }\) = \(\frac { 0.18 }{ 1.10 }\) = \(\frac { 18 }{ 110 }\) = \(\frac { 9 }{ 55 }\)
and \(\frac { PF }{ FR }\) = \(\frac { 0.36 }{ 2.20 }\) = \(\frac { 36 }{ 220 }\) = \(\frac { 9 }{ 55 }\)
So, \(\frac { PE }{ EQ }\) = \(\frac { PF }{ FR }\)
Thus, EF divides sides PQ and PR of ∆ PQR in the same ratio. Therefore, by the converse of Basic Proportionality Theorem, we have EF || QR.
![]()
Question 3.
In the figure, if LM || CB and LN || CD, prove that \(\frac { AM }{ AB }\) = \(\frac { AN }{ AD }\)
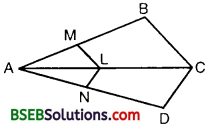
Solution:
In ∆ ABC, we have :
LM || CB
∴By a result based on Basic Proportionality Theorem (a corollary), we have :
\(\frac { AM }{ AB }\) = \(\frac { AL }{ AC }\) … (1)
In ∆ ACD, we have :
LN || CD [Given]
∴By a result based on Basic Proportionality Theorem, we have :
\(\frac { AL }{ AC }\) = \(\frac { AN }{ AD }\)
From (1) and (2), we obtain that
\(\frac { AM }{ AB }\) = \(\frac { AN }{ AD }\)
Question 4.
In the figure, DE || AC and DF || AE. Prove that \(\frac { BF }{ FE }\) = \(\frac { BE }{ EC }\)
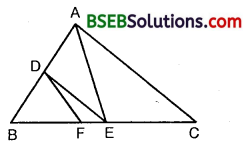
Solution:
In ∆ BGA, we have :
DE || ‘AC
∴By Basic Proportionality Theorem, we have :
\(\frac { BE }{ EC }\) = \(\frac { BD }{ DA }\) …. (1)
In ∆ BEA, we have :
DF || AE [Given]
∴By Basic Proportionality Theorem, we have
\(\frac { BF }{ FE }\) = \(\frac { BD }{ DA }\) …. (2)
From (1) and (2), we obtain that
\(\frac { BF }{ FE }\) = \(\frac { BE }{ EC }\).
Question 5.
In the figure, DE || OQ and DF || OR. Show that EF || QR.
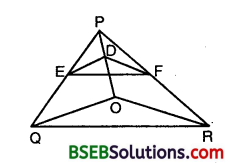
Solution:
In ∆ PQO, we have :
DE || OQ [Given]
∴By Basic Proportionality Theorem, we have :
\(\frac { PE }{ EQ }\) = \(\frac { PD }{ DO }\) … (1)
In ∆ POR, We have :
DF || OR [Given]
∴By Basic Proportionality Theorem, we have
\(\frac { PD }{ DO }\) = \(\frac { PF }{ FR }\) … (2)
From (1) and (2), we obtain that
\(\frac { PE }{ EQ }\) = \(\frac { PF }{ FR }\)
So, EF || QR [By the converse of BPT]
![]()
Question 6.
In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
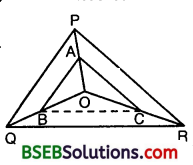
Solution:
Given : O is any point within ∆ PQR, AB || PQ and AC || PR
To prove : BC || QR.
Construction : Join BC.
Proof:
In ∆ OPQ, we have :
AB || PQ [Given]
∴By Basic Proportionality Theorem, we have :
\(\frac { OA }{ AP }\) = \(\frac { OB }{ BQ }\) … (1)
In ∆ OPR, We have :
AC || PR [Given]
∴ By Basic Proportionality Theorem, we have
\(\frac { OA }{ AP }\) = \(\frac { OC }{ CR }\) … (2)
From (1) and (2), we obtain that
\(\frac { OB }{ BQ }\) = \(\frac { OC }{ CR }\)
Thus, in ∆ OQR, B and C are points dividing the sides OQ and OR in the same ratio. Therefore, by the converse of Basic Proportionality Theorem, we have :
BC || QR.
Question 7.
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
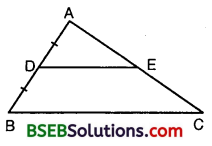
Solution:
Given : ∆ ABC, in which D is the mid-point of side AB and the line DE is drawn parallel to BC, meeting AC in E.
To prove : AE = EC
Proof:
Since DE || BC, therefore by Basic Proportionality Theorem, we have :
\(\frac { AD }{ DB }\) = \(\frac { AE }{ EC }\) … (1)
But AD = DB [∵D is the mid-point of AB]
i.e., \(\frac { AD }{ DB }\) = 1
∴ From (1), \(\frac { AE }{ EC }\) = 1 or AE = EC
Hence, E is the mid-point of the third side AC.
![]()
Question 8.
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
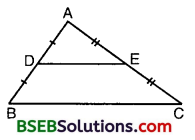
Solution:
Given : ∆ ABC, in which D and E are the mid¬points of sides AB and AC respectively.
To prove : DE || BC.
Proof :
Since D and E are the mid-points of AB and AC respectively, therefore
AD = DB and AE = EC
Now, AD = DB
∴ \(\frac { AD }{ DB }\) = 1
and AE = EC
∴ \(\frac { AE }{ EC }\) = 1
Thus, in ∆ ABC, D and E are points dividing the sides AB and AC in the same ratio. Therefore, by the converse of Basic Proportionality Theorem (Theorem 6.2), we have :
DE || BC.
Question 9.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\).
Solution:
Given : A trapezium ABCD, in which AB || DC and its diagonals AC and BD intersect each other at O.
To prove : \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\).
Construction : Through O, draw OE || AB, i.e., OE || DC.
Proof:
In ∆ ADC, we have :
OE || DC [Construction]
∴ By Basic Proportionality Theorem, we have :
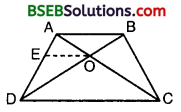
\(\frac { AE }{ ED }\) = \(\frac { AO }{ CO }\) … (1)
Again, in ∆ ABD, we have :
OE || AB [Construction]
∴By Basic Proportionality Theorem, we have :0
\(\frac { ED }{ AE }\) = \(\frac { DO }{ BO }\) or \(\frac { AE }{ ED }\) = \(\frac { BO }{ DO }\) … (2)
From (1) and (2), we obtain that
\(\frac { AO }{ CO }\) = \(\frac { BO }{ DO }\) or \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\).
![]()
Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\) that ABCD is a trapezium.
Solution:
Given : A quadrilateral ABCD in which its diagonals AC and BD intersect each other at the point O such that \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\), i.e., \(\frac { AO }{ CO }\) = \(\frac { BO }{ DO }\)
To prove : Quadrilateral ABCD is a trapezium.
Construction : Through O, draw OE || AB meeting AD in E.
Proof:
In ∆ ADB, we have :
OE || AB [Construction]
∴ By Basic Proportionality Theorem, we have :
\(\frac { DE }{ EA }\) = \(\frac { OD }{ BO }\)
or \(\frac { EA }{ DE }\) = \(\frac { BO }{ DO }\)
i.e., \(\frac { EA }{ DE }\) = \(\frac { BO }{ DO }\) = \(\frac { AO }{ CO }\) [ ∵\(\frac { AO }{ CO }\) = \(\frac { BO }{ DO }\)(given)]
or \(\frac { EA }{ DE }\) = \(\frac { AO }{ CO }\)
Thus, in ∆ ADC, points E and O are dividing the sides AD and AC in the same ratio. Therefore, by the converse of Basic Proportionality Theorem, we have :
EO || DC
But, EO || AB [construction]
Hence, AB || DC
∴ Quadrilateral ABCD is a trapezium