Bihar Board Class 10th Maths Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1 Textbook Questions and Answers.
BSEB Bihar Board Class 10th Maths Solutions Chapter 9 Some Applications of Trigonometry Ex 9.1
![]()
Question 1.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see figure).
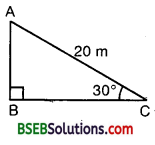
Solution:
In rt ∆ ABC, \(\frac { AB }{ AC }\) = sin 30°
So, \(\frac { AB }{ 20 }\) = \(\frac { 1 }{ 2 }\)
or AB = \(\frac { 1 }{ 2 }\) x 20 m = 10 m
∴ Height of the pole is 10 m.
Question 2.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution:
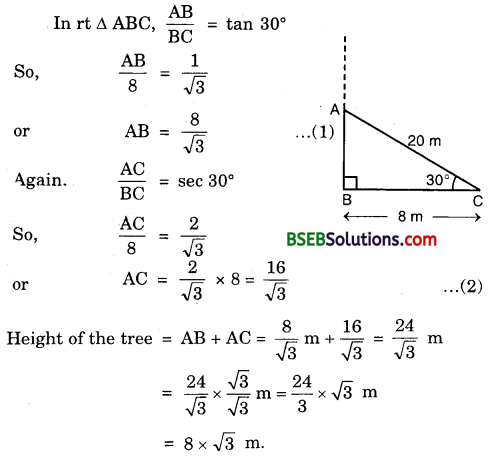
Question 3.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution:
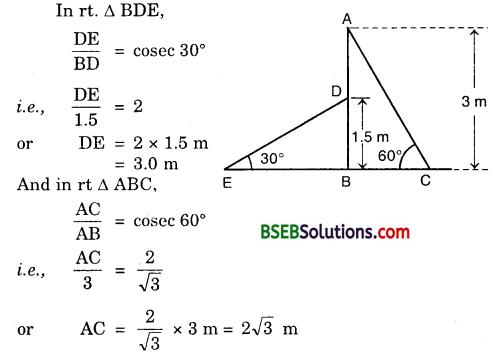
∴ Length of the two slides are 3 m and 2\(\sqrt{3}\) m respectively.
Question 4.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution:
Let AB be the tower of height h metres and let C be a point at a distance of 30 m from the foot of the tower. The angle of elevation of the top of the tower from point C is given as 30°.
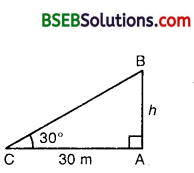
In ∆ CAB, we have :
\(\frac { AB }{ CA }\) = tan 30°. So, \(\frac { h }{ 30 }\) = \(\frac{1}{\sqrt{3}}\)
or h = \(\frac{30}{\sqrt{3}}\) = 10\(\sqrt{3}\)
Hence, the height of the tower is 10-73 metres.
![]()
Question 5.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Let OA be the horizontal ground, and let K be the position of the kite at height 60 m above the ground. Let the length of the string OK be x metres. It is given that ∠KOA = 60°.
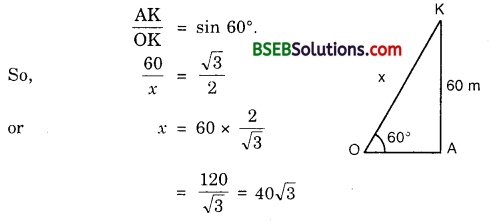
Hence, the length of the string is 40\(\sqrt{3}\) m.
Question 6.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Let OA be the building and PL’be the initial position of the boy such that ∠APR = 30° and AO = 30 m. Let MQ be the position of the boy after walking a distance PQ. Here, ∠AQR = 60°.
Now from ∆s ARQ and ARP, we have :

Hence, the distance walked by the boy towards the building is 19\(\sqrt{3}\) metres.
![]()
Question 7.
From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:
Let BC be the building of height 20 m and CD be the tower of height x metres.
Let A be a point on the ground at a distance of y metres away from the foot B of the building.
In ∆ ABC, we have :
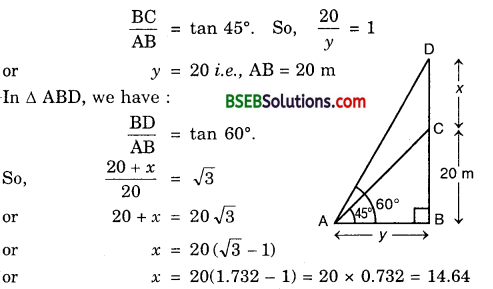
Hence, the height of the tower is 14.64 metres.
Question 8.
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:
Let BC be the pedestal of height h metres and CD be the statue of height 1.6 m.
Let A be a point on the ground such that ∠CAB = 45° and ∠DAB = 60°.
From ∆s ABC and ABD, we have :
\(\frac { AB }{ BC }\) = cot 45°. So, \(\frac { AB }{ h }\) = 1
or AB = h … (1)
\(\frac { Bd }{ AB }\) = tan 60°. So, \(\frac { BC+CD }{ AB }\) = \(\sqrt{3}\)
or \(\frac { h+1.6 }{ h }\) = \(\sqrt{3}\) or h + 1.6 = h\(\sqrt{3}\)
or h(\(\sqrt{3}\) – 1) = 1.6
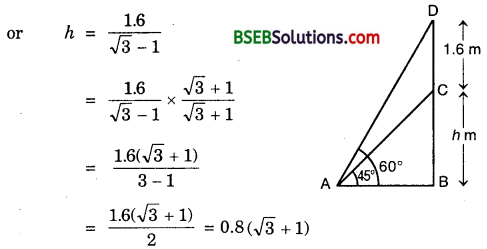
0.8(\(\sqrt{3}\) + 1) = 0.8(1.732 + 1) m = 2.19 m.
Question 9.
The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB be the building of height h metres and AC, the horizontal ground through C, the foot of the tower. Since the building subtends an angle of 30° at C, hence ∠ACB = 30°. Let CD be the tower of 50 m height 50 m such that ∠CAD = 60°.
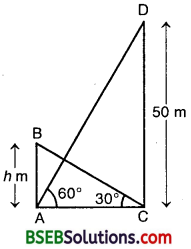
From ∆s BAC and DCA, we have :
So, \(\frac { AC }{ h }\) = \(\sqrt{3}\)
or AC = \(\sqrt{3}\) … (1)
and, \(\frac { DC }{ AC }\) = tan 60°. So, \(\frac { 50}{ AC }\) = \(\sqrt{3}\)
or AC = \(\frac{50}{\sqrt{3}}\)
or AC = \(\frac{50}{\sqrt{3}}\) … (2)
Equating the values of AC from (1) and (2), we get
\(\sqrt{3}\)h = \(\frac{50}{\sqrt{3}}\)
or h = \(\frac{50}{\sqrt{3}}\) x \(\frac{1}{\sqrt{3}}\) = \(\frac { 50}{ 3 }\) = 16\(\frac { 2}{ 3 }\)
Hence, the height of the building is 16\(\frac { 2}{ 3 }\)m.
Question 10.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.
Solution:
Let AB and CD be two poles, each of height h metres. Let P be a point on the road such that AP = x metres. Then, CP = (80 – x) metres. It is given that
∠APB = 60° and ∠CPD = 30°.
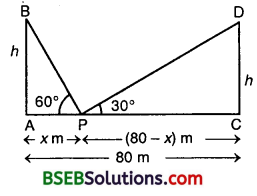
In ∆ APB, we have :
\(\frac { AB }{ AP }\) = tan 60°. So, \(\frac { h}{ x }\) = \(\sqrt{3}\)
or h = \(\sqrt{3}\) x
In ∆ CPD, we have :
\(\frac { CD }{ CP }\) = tan 30°. So, \(\frac { h}{ 80-x }\) = \(\frac{1}{\sqrt{3}}\)
or h = \(\frac{80-x}{\sqrt{3}}\)
Equating the values of h from (1) and (2), we get
\(\sqrt{3}\)x = \(\frac{80-x}{\sqrt{3}}\) or 3x = 80 – x
So, 4x = 80 or x = 20
Putting x = 20 in (1), we get
h = \(\sqrt{3}\) x 20 = (1.732) x 20 = 34.64
Thus, the height of the pole is 34.64 metres. Further, the required point is at a distance of 20 metres from the first pole and 60 metres from the second pole.
![]()
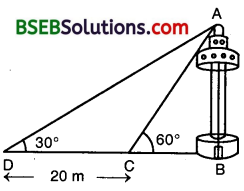
Question 11.
A T.V. tower stands vertically on a bank of a river. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away from this point on the same bank, the angle of elevation of the top of the tower is 30° (See figure). Find the height of the tower and the width of the river.
Solution:
Let AB be the T.V. tower of height h metres standing on the bank of a river. Let C be the point on the opposite bank of the river such that BC = x metres. Let D be another point away from C such that CD = 20 m, ancLthe angles of elevation of the top of the T.V. tower from C and D are 60° and 30° respectively, i.e., ∠ACB = 60° and ∠ADB = 30°.
In ∆ ABC, we have :
Equating values of h from (1) and (2), we get
\(\sqrt{3}\)x + \(\frac{x+20}{\sqrt{3}}\) or 3x = x + 20
or 3x – x = 20 or 2x = 20 or x = 10
Putting x = 10 in (1), we get
h = \(\sqrt{3}\) x 10 = (1.732) x 10 = 17.32
Thus, the height of the T.V. tower is 17.32 metres and the width of the river is 10 metres.
Question 12.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let AB be the building of height 7 metres and let CD be the cable tower. It is given that the angle of elevation of the top D of the tower observed from A is 60° and the angle of depression of the base G of the tower observed from A is 45°.
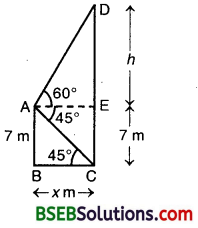
Then, ∠EAD = 60° arid ∠EAC = 45°. Therefore,
∠BCA = ∠EAC = 45°.
Also, AB = 7 m.
In ∆ EAD, we have :
\(\frac { DE }{ EA }\) = tan 60°
So, \(\frac { h }{ x }\) = \(\sqrt{3}\)
or h = \(\sqrt{3}\)x … (1)
In ∆ ABC, we have :
\(\frac { AB }{ BC }\) = tan 45°. So, \(\frac { 7 }{ x }\) = 1
or x = 7
Putting x = 7 in (1), we get
h = 7\(\sqrt{3}\)
So, DE = 7\(\sqrt{3}\) m
∴ CE + ED = (7 + 7 \(\sqrt{3}\)) m
= 7(\(\sqrt{3}\) + 1) m = 7(1.732 + 1) m
= 7 x 2.732 m = 19.124 m
Hence, the height of the cable tower is 19.124 m.
Question 13.
As observed from the top of a 75 m tall lighthouse, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
[Annual Paper (Outside Delhi) 2008]
Solution:
Let AB be the lighthouse of height 75 m and let two ships be at C and D such that their angles of depression B are 45° and 30° respectively.
Let AC = x and CD = y.

In ∆ ABC, we have :
\(\frac { AB }{ AC }\) = tan 45°.
So, \(\frac { 75 }{ x }\) = 1
or x = 75 … (1)
In ∆ ABD, we have :
\(\frac { AB }{ AD }\) = tan 30°.
So, \(\frac { 75 }{ x+y }\) = \(\frac{1}{\sqrt{3}}\)
or x + y = 75\(\sqrt{3}\) … (2)
From (1) and (2), we have :
75 + y = 75\(\sqrt{3}\) or y = 75(\(\sqrt{3}\) – 1)
or y = 75(1.732 – 1) = 75 x 0.732 = 54.9
Hence, the distance between the two ships is 54.9 metres.
![]()
Question 14.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.
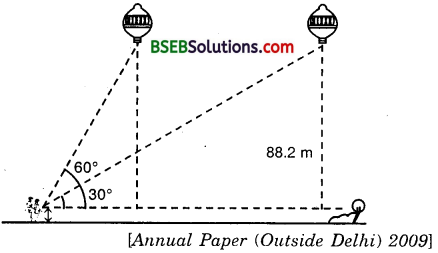
Solution:
Let P and Q be the two positions of the balloon and let A be the point of observation. Let ABC be the horizontal through A. It is given that angles of elevation of the balloon in two positions P and Q from A are ∠PAB = 60° and ∠QAB = 30°. It is also given that
MQ = 88.2 m gives CQ = MQ – MC = (88.2 – 1.2) m = 87 metres.
In ∆ ABP, we have :
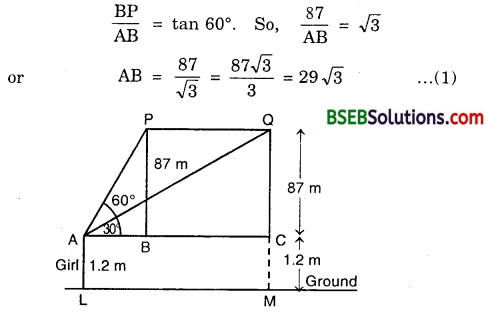
In ∆ ACQ, we have :
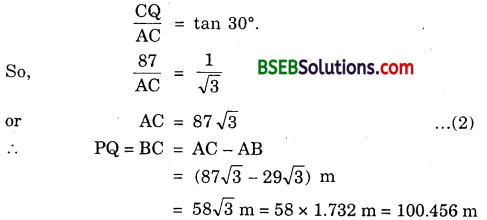
Thus, the balloon travels 100.46 metres during the given interval.
Question 15.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six minutes later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower.
Solution:
Let AB be the tower of height h. Let C be the initial position of the car and let after 6 minutes, the car be at D. It is given that the angles of depression at C and D are 30° and 60° respectively. Let the speed of the car be v metres per minute. Then,
CD = Distance travelled by the car in 6 minutes.
or CD = 6v metres [∵ Distance = Speed x Time]
. Let the car takes t minutes to reach the foot of the tower AB from D. Then,
DA = vt metres
In ∆ ABD, we have :
\(\frac { AB }{ AD }\) = tan 60°
or \(\frac { h }{ vt }\) = \(\sqrt{3}\) vt …. (1)
In ∆ ABC, we have :
\(\frac { AB }{ AC }\) = tan 30° or \(\frac { h }{ vt+6v }\) = \(\frac{1}{\sqrt{3}}\)
or \(\sqrt{3}\) h = vt + 6v
Substituting the value of h from (1) in (2),
we get \(\sqrt{3}\) x \(\sqrt{3}\) vt = vt + 6v
or 3t = t + 6
or 3t – t = 6 or 2t = 6 or t = 3
Thus, the car will reach the tower from D in 3 minutes.
![]()
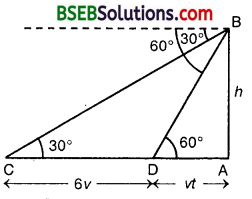
Question 16.
The angle of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Let AB be the tower. Let C and D be the two points at distances 9 m and 4 m respectively from the base of the tower. Then, AC = 9 m and AD = 4 m.
Let ∠ACB = 0 then ∠ADB = 90° – 0.
[∵ Angles are complementry]
Let h metres be the height of the tower AB.
From ∆ ACB, we have :
\(\frac { AB }{ AC }\) = tan θ
or \(\frac { h }{ 9 }\) = tan θ … (1)
From ∆ ADB, we have :
\(\frac { AB }{ AD }\) = tan (90° – θ)
or \(\frac { h }{ 4 }\) = cot θ … (2)
From (1) and (2), we have : h h
\(\frac { h }{ 9 }\) x \(\frac { h }{ 4 }\) = tan θ x cot θ
or h² = 36 or h = 6
Hence, the height of the tower is 6 metres.